Page 75 - Libro Hipertextos Fisica 1

Componente: Procesos físicos

EJEMPLO

Una persona se mueve sobre una plataforma en dirección perpendicular a la dirección de esta. Si la veloci-
dad de la plataforma es 12 km/h y la velocidad de la persona es de 2 m/s, determinar la velocidad (norma
y dirección) con que la persona se mueve con respecto a la vía.
Solución:
Primero se deben expresar todas las magnitudes en las mismas unidades de medida. Así:
12 km 1.000m 1h
12 km h 5 ? ? 5 3,3m sFactoresdeconversión
h 1km 3.600s
La dirección del movimiento de la plataforma es perpendicular
a la dirección del movimiento de la persona. Por tanto,
de la gráfica de la situación se puede ver que v es la hipotenusa
de un triángulo rectángulo. Así v
v 0
v (3,3 m/s) 2 (2 m/s) 2 3,9m/s

Para determinar la medida del ángulo a, tenemos
2 ms catetoopuesto v
tan v 0 0,513 Puuestan p
v p 3,9 ms catetoadyacente
Luego a 5 tan 0,513 5 27,1°
21
En conclusión, la persona se desplaza respecto a la vía con una velocidad de 3,9 m/s, en la dirección determinada
por el ángulo de 27,1° con respecto a la dirección de movimiento de la plataforma.

Caso 4. Composición de movimientos uniformes

cuyas direcciones forman un ángulo determinado
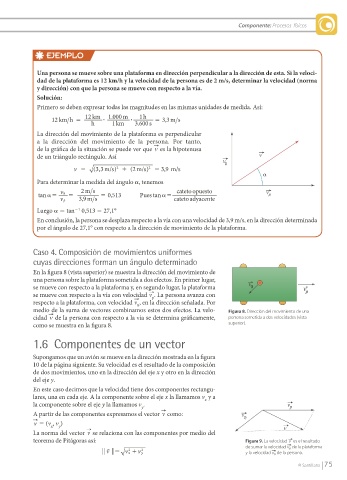
En la figura 8 (vista superior) se muestra la dirección del movimiento de
una persona sobre la plataforma sometida a dos efectos. En primer lugar,
se mueve con respecto a la plataforma y, en segundo lugar, la plataforma
se mueve con respecto a la vía con velocidad v . La persona avanza con
p
respecto a la plataforma, con velocidad v , en la dirección señalada. Por
0
medio de la suma de vectores combinamos estos dos efectos. La velo- Figura 8. Dirección del movimiento de una
cidad v de la persona con respecto a la vía se determina gráficamente, persona sometida a dos velocidades (vista
como se muestra en la figura 8. superior).

1.6 Componentes de un vector

Supongamos que un avión se mueve en la dirección mostrada en la figura
10 de la página siguiente. Su velocidad es el resultado de la composición
de dos movimientos, uno en la dirección del eje x y otro en la dirección
del eje y.
En este caso decimos que la velocidad tiene dos componentes rectangu-
lares, una en cada eje. A la componente sobre el eje x la llamamos v y a
x
la componente sobre el eje y la llamamos v . v
y p
A partir de las componentes expresamos el vector v como: v 0
v 5 (v , v ) v
y
x
La norma del vector v se relaciona con las componentes por medio del
teorema de Pitágoras así: Figura 9. La velocidad v es el resultado
v  v x v 2 y de sumar la velocidad v p de la plataforma
2
y la velocidad v 0 de la persona.
© Santillana 75

FI10-U3(68-85).indd 75 4/10/10 12:47