Page 72 - Libro Hipertextos Fisica 1

Magnitudes vectoriales

De manera análoga, como el desplazamiento en el plano se representa
y
por el vector D r , definimos la velocidad media como:
 r 
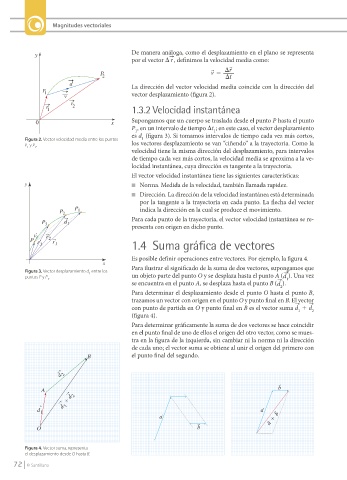
P 2 v t
d La dirección del vector velocidad media coincide con la dirección del
P 1
v vector desplazamiento (figura 2).
r
r 2
1 1.3.2 Velocidad instantánea
0 x Supongamos que un cuerpo se traslada desde el punto P hasta el punto
P , en un intervalo de tiempo Dt ; en este caso, el vector desplazamiento
1
1
es d (figura 3). Si tomamos intervalos de tiempo cada vez más cortos,
Figura 2. Vector velocidad media entre los puntos 1
P y P . los vectores desplazamiento se van “ciñendo” a la trayectoria. Como la
1 2
velocidad tiene la misma dirección del desplazamiento, para intervalos
de tiempo cada vez más cortos, la velocidad media se aproxima a la ve-
locidad instantánea, cuya dirección es tangente a la trayectoria.
El vector velocidad instantánea tiene las siguientes características:
y n Norma. Medida de la velocidad, también llamada rapidez.
n Dirección. La dirección de la velocidad instantánea está determinada
por la tangente a la trayectoria en cada punto. La flecha del vector
P
P 2 1 indica la dirección en la cual se produce el movimiento.
P 3 d 1 Para cada punto de la trayectoria, el vector velocidad instantánea se re-
presenta con origen en dicho punto.
v r
P r 3 2 r 1 1.4 Suma gráfica de vectores

Es posible definir operaciones entre vectores. Por ejemplo, la figura 4.
x
Figura 3. Vector desplazamiento d entre los Para ilustrar el significado de la suma de dos vectores, supongamos que
1
puntos P y P . 1 un objeto parte del punto O y se desplaza hasta el punto A (d ). Una vez
1
se encuentra en el punto A, se desplaza hasta el punto B (d ).
2
Para determinar el desplazamiento desde el punto O hasta el punto B,
trazamos un vector con origen en el punto O y punto final en B. El vector
con punto de partida en O y punto final en B es el vector suma d 1 d
1
2
(figura 4).
Para determinar gráficamente la suma de dos vectores se hace coincidir
en el punto final de uno de ellos el origen del otro vector, como se mues-
tra en la figura de la izquierda, sin cambiar ni la norma ni la dirección
de cada uno; el vector suma se obtiene al unir el origen del primero con
B el punto final del segundo.

d 2

b
A
d 2

d 1
d 1 a
a a b

O b

Figura 4. Vector suma, representa
el desplazamiento desde O hasta B.
72 © Santillana

FI10-U3(68-85).indd 72 4/10/10 12:46