Page 55 - Fisica General Burbano

OSCILACIONES 63

A : distancia máxima a la posición de equilibrio; para la ecuación del oscilador que hemos
0
propuesto la adquiere cuando t =0,si j =0 (Fig. III-35) y, para t =t (j ¹0) en el
1
caso de la Fig. III-36.
w: Frecuencia angular constante del oscilador amortiguado, característica propia del oscila-
dor. Haciendo w =2pn, la frecuencia del oscilador será constante y su inversa G, tam-
bién lo será.
k: la llamamos «ÍNDICE DE AMORTIGUAMIENTO» y es también una característica propia del osci-
lador.
j: FASE INICIAL que para t =0 Þ x =A cos j Þ cos j =x /A.
0
0

MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR

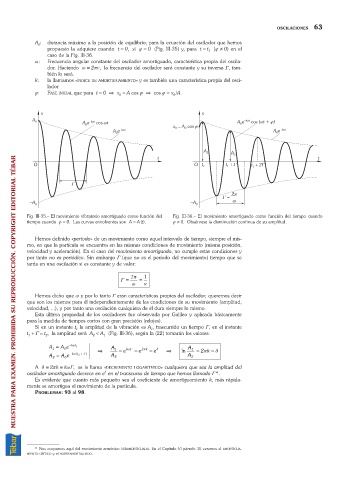
Fig. III-35.– El movimiento vibratorio amortiguado como función del Fig. III-36.– El movimiento amortiguado como función del tiempo cuando
tiempo cuando j =0. Las curvas envolventes son A =A(t). j ¹0. Obsérvese la disminución continua de su amplitud.

Hemos definido «período» de un movimiento como aquel intervalo de tiempo, siempre el mis-
mo, en que la partícula se encuentra en las mismas condiciones de movimiento (misma posición,
velocidad y aceleración). En el caso del movimiento amortiguado, no cumple estas condiciones y
por tanto no es periódico. Sin embargo G (que no es el período del movimiento) tiempo que se
tarda en una oscilación si es constante y de valor:

2p 1
G = =
w n
Hemos dicho que w y por lo tanto G eran características propias del oscilador; queremos decir
que son los mismos para él independientemente de las condiciones de su movimiento (amplitud,
velocidad, ...), y por tanto una oscilación cualquiera de él dura siempre lo mismo.
Esta última propiedad de los osciladores fue observada por Galileo y aplicada básicamente
para la medida de tiempos cortos con gran precisión (relojes).
Si en un instante t la amplitud de la vibración es A , trascurrido un tiempo G, en el instante
1
1
t +G =t , la amplitud será A <A (Fig. III-36), según la (22) tomarán los valores:
2
2
1
1
kt 1
A = A e - w Þ A 1 = e kwG = e 2p k = e d Þ ln A 1 = 2p k = d
1
0
A = A e - kw ( t 1 + )G A 2 A 2
2
0
A d =2pk =kwG, se le llama «DECREMENTO LOGARÍTMICO» cualquiera que sea la amplitud del
oscilador amortiguado decrece en e en el transcurso de tiempo que hemos llamado G *.
d
Es evidente que cuanto más pequeño sea el coeficiente de amortiguamiento k, más rápida-
mente se amortigua el movimiento de la partícula.
PROBLEMAS:93 al 98.

* Nos ocupamos aquí del movimiento armónico SUBAMORTIGUADO. En el Capítulo VI párrafo 10 veremos el AMORTIGUA-
MIENTO CRÍTICO y el SOBREAMORTIGUADO.