Page 51 - Fisica General Burbano

OSCILACIONES 59

dará como resultante: y
x =åx =sen wt å A cos j +cos wt å A sen j =A sen (wt +j) y y( )t = x + y sen ( wt + j)
0
0
i
i
i
i
i
en la que: M
y 0
å A sen j
tg j = i i x
å A cos j i 0
i
n n n n
2 2 y
-)
A = å A i +å å AA cos (j i - )j j =å å AA cos (j i j j m
j
i
j
i
i = 1 j = 1 i = 1 j = 1
i ¹ j O t
T T
CASOS PARTICULARES: 2
1.º La diferencia de fase (j – j ) es cero ó 2Kp (K Î Z): ello quiere decir que si por la prime-
2
1
ra causa el punto pasa en el instante inicial por origen y hacia arriba, también por la segunda cau- Fig. III-24.– La magnitud variable
con el tiempo armónicamente puede
sa hará lo mismo en tal instante. tomar siempre valores positivos.
Al ser cos 2Kp =1 el valor de A dado por (19) es:
2 2 2 2
A = A 1 + A 2 + 2 A A 2 =( A 1 A + ) Þ A A = 1 A+ 2
2
1
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
Resulta así la amplitud máxima o sea la suma de las amplitudes. La representación gráfica del
movimiento sería la de la Fig. III-25. La ecuación de la vibración armónica resultante es:
x =(A +A ) sen (wt +j)
1
2
2.º La diferencia de fase es p ó(2K +1) p (K Î Z): ello quiere decir que si por la primera
causa el punto pasa en el instante inicial por el origen y hacia arriba, por la segunda causa lo hará
por el origen y hacia abajo. Al ser cos (2K +1) p =–1, el valor de A dado por (19) es:
2 2 2 2
A = A 1 + A 2 - 2 A A 2 =( A 1 A - ) Þ A A = 1 A- 2
2
1
con A >A . Resulta así la amplitud mínima o sea la diferencia de las amplitudes (Fig. III-26). La Fig. III-25.– Composición de MAS de
2
1
ecuación de la vibración armónica resultante es: la misma frecuencia y dirección
cuando Dj =2Kp.
x =(A – A ) sen (wt +j)
2
1
En el caso A =A , el punto queda en reposo.
1
2
3.º La diferencia de fase es p/2 ó(2K +1) p/2,(K Î Z): en este caso se dice que los dos mo-
vimientos vibratorios armónicos componentes se encuentran en «CUADRATURA». Al ser
cos (2K +1)p/2 =0, el valor de A dado por (19) es:
2 2 2
A = A 1 + A 2
y la (18) la podemos escribir:
A
tg j + A 2
1
(
tg j = A 1 = tg j + )
F
1
1 - 2 tg j 1
A 1 Fig. III-26.– Composición de MAS de
en la que hemos sustituido A /A =tg F, resultando: la misma frecuencia y dirección
1
2
cuando Dj =(2K +1) p.
A
j = j +F = j 1 +arctg 2
1
A 1
y la vibración armónica resultante:
x j - j =( 2K 1 +) p
2
1
2
x = A 1 2 + A sen (w t +j 1 + )F A 2
2
A
2
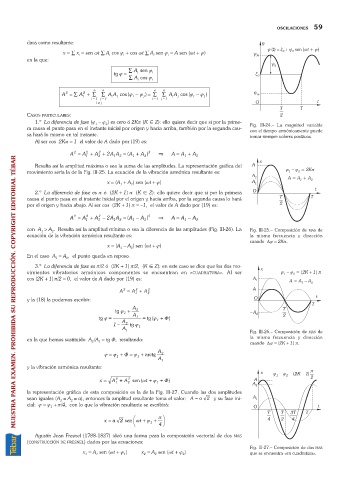
la representación gráfica de esta composición es la de la Fig. III-27. Cuando las dos amplitudes
sean iguales (A =A =a), entonces la amplitud resultante toma el valor: A = a 2 y su fase ini- A 1
2
1
cial: j =j +p/4, con lo que la vibración resultante se escribirá: O t
1
F p I T T 3T T
x = a 2 sen H G w t +j 1 + J K 4 2 4
4
Agustín Jean Fresnel (1788-1827) ideó una forma para la composición vectorial de dos MAS
(CONSTRUCCIÓN DE FRESNEL) dados por las ecuaciones:
Fig. III-27.– Composición de dos MAS
x =A sen (wt +j ) x =A sen (wt +j ) que se encuentra «en cuadratura».
1
1
1
2
2
2