Page 47 - Fisica General Burbano

MOVIMIENTOS RECTILÍNEOS UNIFORME Y UNIFORMEMENTE ACELERADO 55

haciendo t =0, C =v velocidad cuando el tiempo es cero o velocidad inicial; el valor de v es x
0
por tanto: v =v +at. Como v =dx/dt Þ dx =vdt, obtenemos:
0
zz v 0 + at dt =) v 0 z z t dt Þ x = v t a + t 2 2 C+¢ (a)
a
dx = (
dt +
0
2
haciendo t =0 Þ C¢=x o posición inicial; el valor de x es, por tanto: x =x +v t +at /2. x = x + v t + 1 at 2
0
0
0
Una expresión especialmente útil en la resolución de problemas de este tipo de movimiento es x 0 0 0 2
la que nos relaciona directamente posiciones, velocidades y aceleración. Si en las expresiones (12)
eliminamos el tiempo, tenemos: t =(v – v )/a con lo que: t
0
O
v ( v - v ) av - v ) 2 2
(
x
x - x 0 = 0 0 + 0 Þ v= ± v 0 +2a ( x - )
0
a 2a 2 v
Todas las expresiones anteriores, con sus casos particulares de v =0, x =0 ó ambos, son (b)
0
0
válidas tanto si la aceleración es positiva como negativa. En cada caso particular bastará con susti- v + at
tuir a por su valor numérico con el signo correspondiente. Cuando a <0, el movimiento se suele v = 0
llamar decelerado.
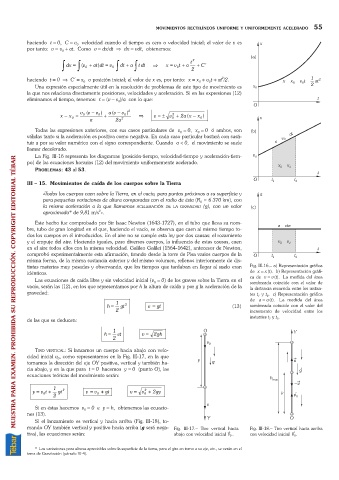
La Fig. III-16 representa los diagramas (posición-tiempo, velocidad-tiempo y aceleración-tiem- v 0
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
po) de las ecuaciones horarias (12) del movimiento uniformemente acelerado.
x - x
PROBLEMAS: 43 al 53. 2 1
t
O t t
III – 15. Movimientos de caída de los cuerpos sobre la Tierra 1 2
«Todos los cuerpos caen sobre la Tierra, en el vacío, para puntos próximos a su superficie y a
para pequeñas variaciones de altura comparadas con el radio de ésta (R • 6 370 km), con
0
la misma aceleración a la que llamamos ACELERACIÓN DE LA GRAVEDAD (g), con un valor (c)
2
aproximado* de 9,81 m/s ».
Este hecho fue comprobado por Sir Isaac Newton (1643-1727), en el tubo que lleva su nom-
bre, tubo de gran longitud en el que, haciendo el vacío, se observa que caen al mismo tiempo to- a = cte
dos los cuerpos en él introducidos. En el aire no se cumple esta ley por dos causas: el rozamiento
y el empuje del aire. Haciendo iguales, para diversos cuerpos, la influencia de estas causas, caen v - v 1
2
en el aire todos ellos con la misma velocidad. Galileo Galilei (1564-1642), antecesor de Newton, t
comprobó experimentalmente esta afirmación, tirando desde la torre de Pisa varios cuerpos de la O t t
misma forma, de la misma sustancia exterior y del mismo volumen, rellenos interiormente de dis- 1 2
tintas materias muy pesadas y observando, que los tiempos que tardaban en llegar al suelo eran Fig. III-16.– a) Representación gráfica
idénticos. de x =x(t). b) Representación gráfi-
Las ecuaciones de caída libre y sin velocidad inicial (v =0) de los graves sobre la Tierra en el ca de v =v(t). La medida del área
0
sombreada coincide con el valor de
vacío, serán las (12), en los que representamos por h la altura de caída y por g la aceleración de la la distancia recorrida entre los instan-
gravedad: tes t y t . c) Representación gráfica
2
1
de a =a (t). La medida del área
1 2
h = gt v = gt (13) sombreada coincide con el valor del
2 incremento de velocidad entre los
instantes t y t .
de las que se deducen: 1 2
1 O
h = vt v = 2 gh
2
v ® 0
TIRO VERTICAL: Si lanzamos un cuerpo hacia abajo con velo-
cidad inicial v , como representamos en la Fig. III-17, en la que
0
tomamos la dirección del eje OY positiva, vertical y también ha- y ® g
cia abajo, y en la que para t =0 hacemos y =0 (punto O), las
ecuaciones teóricas del movimiento serán:
1 2 2
y = v t + gt v = v 0 + gt v = v 0 + 2 gy
0
2
®
Si en éstas hacemos v =0 e y =h, obtenemos las ecuacio- v
0
nes (13).
Si el lanzamiento es vertical y hacia arriba (Fig. III-18), to- Y
mando OY también vertical y positivo hacia arriba (g será nega- Fig. III-17.– Tiro vertical hacia Fig. III-18.– Tiro vertical hacia arriba
tiva), las ecuaciones serán: abajo con velocidad inicial v 0 . con velocidad inicial v 0 .
®
®
* Las variaciones para alturas apreciables sobre la superficie de la tierra, para el giro en torno a su eje, etc., se verán en el
tema de Gravitación (párrafo XI-4).