Page 53 - Fisica General Burbano

OSCILACIONES 61

movimiento periódico se puede descomponer, independientemente de su forma, en un de- x
terminado número de funciones armónicas».
El recíproco nos indica que: «si: x =x(t) es una función periódica pero no armónica podemos 1
considerarla como la superposición de movimientos vibratorios armónicos simples de frecuencias
n, 2n, 3n, ..., etc.» (Este análisis de las funciones periódicas fue realizado por el matemático francés 2 t
Joseph Fourier (1780-1830), por lo que la serie trigonométrica que ponemos a continuación lleva O
su nombre). Analíticamente la serie la podemos expresar:

x t( ) = A + A sen 2pn t + A sen 2 2pn t + A sen 2 3pn t ...+ T 2
0
2
3
1
T
Supongamos, por ejemplo, dos movimientos vibratorios armónicos representados por las sinu- 1
soides 1 y 2 (Fig. III-30). El período del primero T , es doble que el segundo, T ; es decir la fre-
1
2
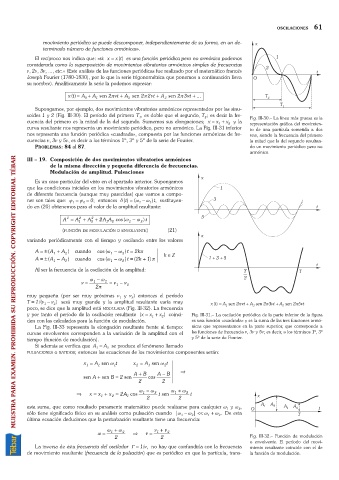
cuencia del primero es la mitad de la del segundo. Sumemos sus elongaciones; x =x +x y la Fig. III-30.– La línea más gruesa es la
representación gráfica del movimien-
1
2
curva resultante nos representa un movimiento periódico, pero no armónico. La Fig. III-31 inferior to de una partícula sometida a dos
nos representa una función periódica «cuadrada», compuesta por las funciones armónicas de fre- MAS, siendo la frecuencia del primero
cuencias n, 3n y 5n, es decir a los términos 1º, 3º y 5º de la serie de Fourier. la mitad que la del segundo resultan-
PROBLEMAS:84 al 87. do un movimiento periódico pero no
armónico.
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
III – 19. Composición de dos movimientos vibratorios armónicos
de la misma dirección y pequeña diferencia de frecuencias.
Modulación de amplitud. Pulsaciones
Es un caso particular del visto en el apartado anterior. Supongamos
que las condiciones iniciales en los movimientos vibratorios armónicos
de diferente frecuencia (aunque muy parecidas) que vamos a compo-
ner son tales que: j =j =0; entonces d(t) =(w – w )t, sustituyen-
2
1
1
2
do en (20) obtenemos para el valor de la amplitud resultante:
2 2 2
A = A 1 + A 2 + 2 A A cos (w 1 -w 2 t )
1
2
(FUNCIÓN DE MODULACIÓN O ENVOLVENTE) (21)
variando periódicamente con el tiempo y oscilando entre los valores
A =± ( A 1 + A ) cuando cos (w 1 - w 2 t ) = 2kp
2
A =± ( A 1 - A ) cuando cos (w 1 - w 2 t ) = (2k + ) 1 p k Î Z
2
Al ser la frecuencia de la oscilación de la amplitud:
w - w 2
1
n = = n - n 2
1
2 p
muy pequeña (por ser muy próximas n y n ) entonces el período
2
1
T =1/(n – n ) será muy grande y la amplitud resultante varía muy
2
1
poco, se dice que la amplitud está MODULADA (Fig. III-32). La frecuencia
y por tanto el período de la oscilación resultante (x =x +x ) coinci- Fig. III-31.– La oscilación periódica de la parte inferior de la figura
2
1
den con las calculadas para la función de modulación. es una función «cuadrada» y es la suma de las tres funciones armó-
La Fig. III-33 representa la elongación resultante frente al tiempo: nicas que representamos en la parte superior, que corresponde a
o
curvas envolventes corresponden a la variación de la amplitud con el las funciones de frecuencia n, 3n y 5n; es decir, a los términos 1 , 3 o
o
tiempo (función de modulación). y 5 de la serie de Fourier.
Si además se verifica que A =A se produce el fenómeno llamado
1
2
PULSACIONES o BATIDOS; entonces las ecuaciones de los movimientos componentes serán:
x = A sen w 1 t x 2 = A sen w 2 t
1
1
1
A + B A - B Þ
2
sen A +sen B = sen cos
2 2
w 1 -w 2 w 1 +w 2
Þ x = x 1 + x 2 = A2 1 cos t sen t
2 2 x
esta suma, que como resultado puramente matemático puede realizarse para cualquier w y w , O A + A 2 A - A 2 t
1
2
1
1
sólo tiene significado físico en su análisis como pulsación cuando |w – w | <<w +w . De esta T
1
2
1
2
última ecuación deducimos que la perturbación resultante tiene una frecuencia:
w + w 2 n + n 2
1
1
w = Þ n=
2 2 Fig. III-32.– Función de modulación
o envolvente. El período del movi-
La inversa de ésta frecuencia del oscilador G =1/n, no hay que confundirla con la frecuencia miento resultante coincide con el de
de movimiento resultante (frecuencia de la pulsación) que es periódico en que la partícula, trans- la función de modulación.