Page 149 - Fisica General Burbano

158 TRABAJO Y ENERGÍA. TEORÍA DE CAMPOS. PRINCIPIO DE CONSERVACIÓN DE LA ENERGÍA

Rw Rw
tg j = 2 = 2 2
(
K - mw m w - w )
0
F F
2 2 2 2 2 0 0
F = A R ( w ) +( K - mw ) Þ A = = (11)
0
2
2
)
)
R ( w ) 2 +( K - mw 2 2 R w 2 + m (w 0 2 -w 2 2
en las que w = Km/ es la FRECUENCIA PROPIA o NATURAL del oscilador libre (sin fuerza externa).
0
El término z = R 2 +(/w - m )w 2 se denomina IMPEDANCIA MECÁNICA del oscilador. Estas
K
ecuaciones nos resuelven el problema de determinar el desfase y la amplitud de las vibraciones
Fig. VII-28.– Construcción de Fresnel. forzadas en función de las características del oscilador y de la fuerza periódica aplicada. Obsérvese
que el sistema vibra con la frecuencia de la fuerza impulsora y no con la frecuencia propia del os-
cilador, resultando un movimiento en el que la amplitud de la oscilación no disminuye.
El movimiento en realidad consta de dos fases (Fig. VII-29), en la primera, (régimen transito-
rio), el efecto del amortiguamiento es apreciable, pero por decaer este con el tiempo, se pasa a
una segunda fase (régimen permanente), que es la analizada hasta aquí y a la que nos referiremos
en adelante.
VII – 30. Fenómenos de resonancia
La expresión (11), indica que la amplitud del oscilador amortiguado y forzado, para un valor
dado de F , depende de la frecuencia de la fuerza impulsora externa. Cuando el valor de la ampli-
0
tud sea máximo diremos que existe resonancia en la amplitud.
Fig. VII-29.– Variación de x con t en «Un sistema entra en RESONANCIA EN LA AMPLITUD cuando para un determinado valor de la
un movimiento vibratorio forzado y frecuencia, la amplitud de las oscilaciones forzadas se hace máxima».
con amortiguamiento.
Obtenemos el valor de la frecuencia de resonancia en la amplitud haciendo mínimo el denomi-
nador de (11): considerando como única variable la pulsación de la fuerza periódica, la derivada
del radicando con respecto a w debe ser nula, es decir:
2
2
R 2w – 2 (K – mw )2mw =0
de donde obtenemos para la pulsación en esta resonancia:
K R 2 2 R 2
w = - = w 0 -
A
m 2m 2 2m 2
y para la frecuencia:

1 K R 2 R 2 MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
n = - = n 2 0 -
A
2
2 p m 2 m 2 8 p m 2
donde w y n son, respectivamente la frecuencia angular y
0
0
la frecuencia propias del oscilador.
Es evidente en estas expresiones, que la frecuencia de
resonancia en la amplitud tiende al valor de la frecuencia
propia del oscilador conforme el coeficiente de amortigua-
miento R se hace más pequeño. En el límite R =0 (oscila-
dor sin amortiguar) se obtiene w =w , y la amplitud
0
A
adopta la expresión:
F F F
A = 0 2 = 2 0 2 = 2 0 2 2
K - mw m w( 0 -w ) 4p m n( 0 -n )
que nos indica que la amplitud es tanto más pequeña
cuanto más diferentes son la frecuencia propia del sistema
no amortiguado (n ) y la de la fuerza externa (n).
0
Representamos en la Fig. VII-30 las curvas de la ampli-
tud en función de la relación entre las frecuencias de la
fuerza externa y la propia del oscilador. En la curva (1), en
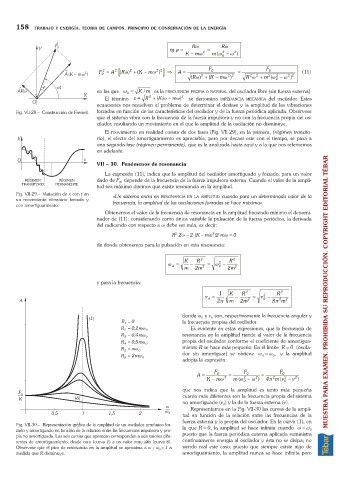
Fig. VII-30.– Representación gráfica de la amplitud de un oscilador armónico for-
zado y amortiguado en función de la relación entre las frecuencias impulsora y pro- la que R =0, la amplitud se hace infinita cuando w =w 0
pia no amortiguada. Las seis curvas que aparecen corresponden a seis valores dife- puesto que la fuerza periódica externa aplicada suministra
rentes de amortiguamiento, desde cero (curva 1) a un valor muy alto (curva 6). continuamente energía al oscilador y ésta no se disipa; no
Obsérvese que el pico de resonancia en la amplitud se aproxima a w / w =1 a siendo real este caso, puesto que siempre existe algo de
0
medida que R disminuye. amortiguamiento, la amplitud nunca se hace infinita pero