Page 143 - Fisica General Burbano

152 TRABAJO Y ENERGÍA. TEORÍA DE CAMPOS. PRINCIPIO DE CONSERVACIÓN DE LA ENERGÍA

«La fuerza que actúa sobre la
partícula en un punto es igual a
menos la pendiente de la curva
de energía potencial».
En las zonas en que U (x) es cre-
ciente su primera derivada es positiva
y, por tanto F negativa (hacia la iz-
quierda); es el caso de posiciones tales
que x < x < x ó x < x < x de la
7
5
3
6
figura. Si la función U (x) es decre-
ciente, F resulta positiva, como en
x < x ó x < x < x . En puntos tales
3
6
5
como x , x , x ,ó x ³x , la pendien-
7
5
3
6
te de U (x) es cero, y por tanto en ellos
la fuerza que actúa sobre la partícula es
nula, son puntos de EQUILIBRIO; si colo-
camos m en x con velocidad nula se
3
queda allí sin moverse. Este equilibrio
es de tres tipos, que llamaremos: EQUI-
LIBRIO ESTABLE, cuando al desplazar la
partícula a izquierda o derecha, la fuer-
za que el campo ejerce sobre ella tien-
de a volverla a la posición de equilibrio
original (es el caso de x =x y x =x );
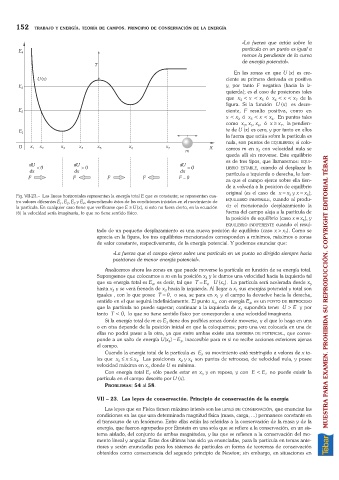
Fig. VII-23.– Las líneas horizontales representan la energía total E que es constante; se representan cua- 3 6
tro valores diferentes E , E , E y E , dependiendo éstos de las condiciones iniciales en el movimiento de EQUILIBRIO INESTABLE, cuando al produ-
1
2
4
3
la partícula. En cualquier caso tiene que verificarse que E ³U(x), si esto no fuera cierto, en la ecuación cir el mencionado desplazamiento la
(6) la velocidad sería imaginaria, lo que no tiene sentido físico. fuerza del campo aleja a la partícula de
la posición de equilibrio (caso x =x ), y
5
EQUILIBRIO INDIFERENTE cuando el resul-
tado de un pequeño desplazamiento es una nueva posición de equilibrio (caso x >x ). Como se
7
aprecia en la figura, los tres equilibrios mencionados corresponden a mínimos, máximos o zonas
de valor constante, respectivamente, de la energía potencial. Y podemos enunciar que:
«La fuerza que el campo ejerce sobre una partícula en un punto va dirigida siempre hacia
posiciones de menor energía potencial».
Analicemos ahora las zonas en que puede moverse la partícula en función de su energía total.
Supongamos que colocamos a m en la posición x y le damos una velocidad hacia la izquierda tal
5
que su energía total es E , es decir, tal que T =E – U (x ). La partícula será acelerada desde x 5
5
4
4
hasta x y se verá frenada de x hacia la izquierda. Al llegar a x sus energías potencial y total son
1
3
3
iguales , con lo que posee T =0, o sea, se para en x y el campo la devuelve hacia la derecha, MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
1
sentido en el que seguirá indefinidamente. El punto x , con energía E , es un PUNTO DE RETROCESO
1
4
que la partícula no puede superar; continuar a la izquierda de x supondría tener U > E y por
1
tanto T < 0, lo que no tiene sentido físico por corresponder a una velocidad imaginaria.
Si la energía total de m es E tiene dos posibles zonas donde moverse, y el que lo haga en una
3
o en otra depende de la posición inicial en que la coloquemos; pero una vez colocada en una de
ellas no podrá pasar a la otra, ya que entre ambas existe una BARRERA DE POTENCIAL, que corres-
ponde a un salto de energía U(x ) – E , inaccesible para m si no recibe acciones exteriores ajenas
3
5
al campo.
Cuando la energía total de la partícula es E su movimiento está restringido a valores de x ta-
2
les que x £x £x . Las posiciones x y x son puntos de retroceso, de velocidad nula, y posee
2
4
2
4
velocidad máxima en x donde U es mínima.
3
Con energía total E sólo puede estar en x y en reposo, y con E < E no puede existir la
1
3
1
partícula en el campo descrito por U (x).
PROBLEMAS: 54 al 58.
VII – 23. Las leyes de conservación. Principio de conservación de la energía
Las leyes que en Física tienen máximo interés son las LEYES DE CONSERVACIÓN, que enuncian las
condiciones en las que una determinada magnitud física (masa, carga, ...) permanece constante en
el transcurso de un fenómeno. Entre ellas están las referidas a la conservación de la masa y de la
energía, que fueron agrupadas por Einstein en una sola que se refiere a la conservación, en un sis-
tema aislado, del conjunto de ambas magnitudes, y las que se refieren a la conservación del mo-
mento lineal y angular. Estas dos últimas han sido ya enunciadas, para la partícula en temas ante-
riores y serán enunciadas para los sistemas de partículas en forma de teoremas de conservación
obtenidos como consecuencia del segundo principio de Newton; sin embargo, en situaciones en