Page 107 - Fisica General Burbano

PROBLEMAS 115

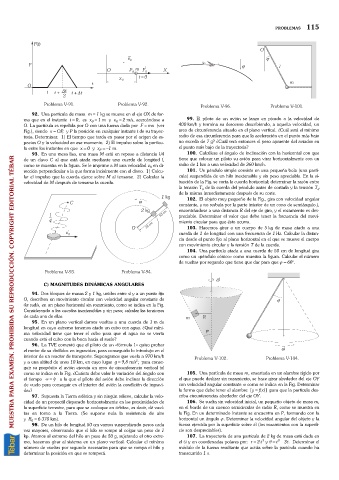
Problema V-91. Problema V-92. Problema V-96. Problema V-101.
92. Una partícula de masa m =1 kg se mueve en el eje OX de for-
ma que en el instante t =0, es x =1 m y v =2 m/s, acercándose a 99. El piloto de un avión se lanza en picado a la velocidad de
0
0
O. La partícula es repelida por O con una fuerza dada por F =mx (ver 400 km/h y termina su descenso describiendo, a aquella velocidad, un
Fig.), siendo x =OP, y P la posición en cualquier instante t de su trayec- arco de circunferencia situado en el plano vertical. ¿Cuál será el mínimo
toria. Determinar: 1) El tiempo que tarda en pasar por el origen de es- radio de esa circunferencia para que la aceleración en el punto más bajo
pacios O y la velocidad en ese momento. 2) El impulso sobre la partícu- no exceda de 7 g? ¿Cuál será entonces el peso aparente del aviador en
la entre los instantes en que x =0 y x =–1 m. el punto más bajo de la trayectoria?
P
93. En una mesa lisa, una masa M está en reposo a distancia l/4 100. Calcúlese el ángulo de inclinación con la horizontal con que
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
de un clavo C al que está atada mediante una cuerda de longitud l, tiene que colocar un piloto su avión para virar horizontalmente con un
como se muestra en la figura. Se le imprime a M una velocidad v 0 en di- radio de 1 km a una velocidad de 360 km/h.
rección perpendicular a la que forma incialmente con el clavo. 1) Calcu- 101. Un péndulo simple consiste en una pequeña bola (una partí-
lar el impulso que la cuerda ejerce sobre M al tensarse. 2) Calcular la cula) suspendida de un hilo inextensible y sin peso apreciable. En la si-
velocidad de M después de tensarse la cuerda. tuación de la Fig. se corta la cuerda horizontal; determinar la razón entre
de la cuerda del péndulo antes de cortarla y la tensión T
la tensión T a d
de la misma inmediatamente después de su corte.
102. El objeto muy pequeño de la Fig., gira con velocidad angular
constante, y no resbala por la parte interior de un cono de semiángulo j,
encontrándose a una distancia R del eje de giro, y el rozamiento es des-
preciable. Determinar el valor que debe tener la frecuencia del movi-
miento circular para que ésto ocurra.
103. Hacemos girar a un cuerpo de 5 kg de masa atado a una
cuerda de 1 de longitud con una frecuencia de 1Hz. Calcular la distan-
cia desde el punto fijo al plano horizontal en el que se mueve el cuerpo
con movimiento circular y la tensión T de la cuerda.
104. Una partícula atada a una cuerda de 50 cm de longitud gira
como un «péndulo cónico» como muestra la figura. Calcular el número
de vueltas por segundo que tiene que dar para que j =60°.
Problema V-93. Problema V-94.

C) MAGNITUDES DINÁMICAS ANGULARES
94. Dos bloques de masas 2 y 1 kg, unidos entre sí y a un punto fijo
O, describen un movimiento circular con velocidad angular constante de
4p rad/s, en un plano horizontal sin rozamiento, como se indica en la Fig.
Considerando a las cuerdas inextensibles y sin peso; calcular las tensiones
de cada una de ellas.
95. En un plano vertical damos vueltas a una cuerda de 1 m de
longitud en cuyo extremo tenemos atado un cubo con agua. ¿Qué míni-
ma velocidad tiene que tener el cubo para que el agua no se vierta
cuando está el cubo con la boca hacia el suelo?
96. La TVE comentó que el piloto de un «fórmula 1» quiso probar
el motor de su «bólido» en ingravidez, para conseguirlo lo introdujo en el
interior de un reactor de transporte. Supongamos que vuela a 970 km/h Problema V-102. Problema V-104.
2
y a una altitud de unos 10 km, en cuyo lugar g =9,8 m/s ; para conse-
guir su propósito el avión ejecuta un arco de circunferencia vertical tal
como se indica en la Fig. ¿Cuánto debe valer la variación del ángulo con 105. Una partícula de masa m, ensartada en un alambre rígido por
.
el tiempo w = j a la que el piloto del avión debe inclinar la dirección el que puede deslizar sin rozamiento, se hace girar alrededor del eje OY
de vuelo para conseguir en el interior del avión la condición de ingravi- con velocidad angular constante w como se indica en la Fig. Determinar
dez? la forma que debe tener el alambre [y =f(x)] para que la partícula des-
97. Supuesta la Tierra esférica y sin ningún relieve, calcular la velo- criba circunferencias alrededor del eje OY.
cidad de un proyectil disparado horizontalmente en las proximidades de 106. Se suelta sin velocidad inicial, un pequeño objeto de masa m,
la superficie terrestre, para que se «coloque en órbita», es decir, dé vuel- en el borde de un cuenco semicircular de radio R, como se muestra en
tas en torno a la Tierra. (Se supone nula la resistencia de aire la Fig. En un determinado instante se encuentra en P, formando con la
y R =6 370 km). horizontal un ángulo j. Determinar la velocidad angular del objeto y la
0
98. De un hilo de longitud 50 cm vamos suspendiendo pesos cada fuerza ejercida por la superficie sobre él (los rozamientos con la superfi-
vez mayores, observando que el hilo se rompe al colgar un peso de 1 cie son despreciables).
kp. Atamos al extremo del hilo un peso de 50 g, sujetando el otro extre- 107. La trayectoria de una partícula de 2 kg de masa está dada en
3
2
mo, hacemos girar al sistema en un plano vertical. Calcular el mínimo el SI y en coordenadas polares por: r =2t y q =t – 3t. Determinar el
número de vueltas por segundo necesarias para que se rompa el hilo y módulo de la fuerza resultante que actúa sobre la partícula cuando ha
determinar la posición en que se romperá. transcurrido 1 s.