Page 82 - Libro Hipertextos Fisica 1

Movimiento de proyectiles

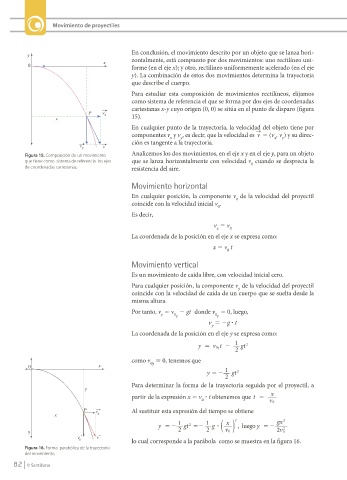
En conclusión, el movimiento descrito por un objeto que se lanza hori-
zontalmente, está compuesto por dos movimientos: uno rectilíneo uni-
forme (en el eje x); y otro, rectilíneo uniformemente acelerado (en el eje
y). La combinación de estos dos movimientos determina la trayectoria
que describe el cuerpo.

Para estudiar esta composición de movimientos rectilíneos, elijamos
como sistema de referencia el que se forma por dos ejes de coordenadas
cartesianas x-y cuyo origen (0, 0) se sitúa en el punto de disparo (figura
15).
En cualquier punto de la trayectoria, la velocidad del objeto tiene por
componentes v y v , es decir, que la velocidad es v 5 (v , v ) y su direc-
x
y
x
y
ción es tangente a la trayectoria.
Analicemos los dos movimientos, en el eje x y en el eje y, para un objeto
Figura 15. Composición de un movimiento
que tiene como sistema de referencia los ejes que se lanza horizontalmente con velocidad v cuando se desprecia la
0
de coordenadas cartesianas. resistencia del aire.
Movimiento horizontal
En cualquier posición, la componente v de la velocidad del proyectil
x
coincide con la velocidad inicial v .
0
Es decir,
v 5 v 0
x
La coordenada de la posición en el eje x se expresa como:

x 5 v t
0
Movimiento vertical

Es un movimiento de caída libre, con velocidad inicial cero.
Para cualquier posición, la componente v de la velocidad del proyectil
y
coincide con la velocidad de caída de un cuerpo que se suelta desde la
misma altura.
Por tanto, v 5 v 2 gt donde v 5 0, luego,
y 0 y 0 y
v 5 2g ? t
y
La coordenada de la posición en el eje y se expresa como:
1
y v t 2 gt 2
0y
como v 5 0, tenemos que
0y
0 x 1
y gt 2
2
Para determinar la forma de la trayectoria seguida por el proyectil, a
y
partir de la expresión x 5 v ? t obtenemos que t 5 x
0 v 0
P v Al sustituir esta expresión del tiempo se obtiene
x x
x
1 1 ( ) 2 gx 2
2
y gt g ? ,luego y 2
y 2 2 v 0 v 2 0
v y v lo cual corresponde a la parábola como se muestra en la figura 16.
Figura 16. Forma parabólica de la trayectoria
del movimiento.
82 © Santillana

FI10-U3(68-85).indd 82 4/10/10 12:47