Page 52 - Libro Hipertextos Fisica 1

El movimiento rectilíneo

Gráfica del desplazamiento-tiempo (x-t)
Como la relación entre el desplazamiento y el tiempo tiene un término
2
cuyo factor es t , entonces la gráfica x-t para el movimiento uniforme-
mente variado es una parábola.
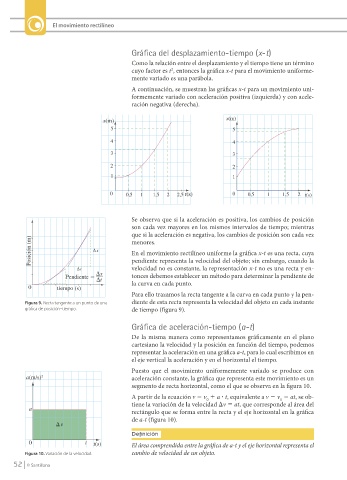
A continuación, se muestran las gráficas x-t para un movimiento uni-
formemente variado con aceleración positiva (izquierda) y con acele-
ración negativa (derecha).

x(m) x(m)
5 5

4 4

3 3
2 2

1 1

0 0,5 1 1,5 2 2,5 t(s) 0 0,5 1 1,5 2 t(s)

Se observa que si la aceleración es positiva, los cambios de posición
son cada vez mayores en los mismos intervalos de tiempo; mientras
que si la aceleración es negativa, los cambios de posición son cada vez
Posición (m) x En el movimiento rectilíneo uniforme la gráfica x-t es una recta, cuya
menores.

pendiente representa la velocidad del objeto; sin embargo, cuando la

t velocidad no es constante, la representación x-t no es una recta y en-
x
Pendiente tonces debemos establecer un método para determinar la pendiente de
t
0 tiempo (s) la curva en cada punto.
Para ello trazamos la recta tangente a la curva en cada punto y la pen-
Figura 9. Recta tangente a un punto de una diente de esta recta representa la velocidad del objeto en cada instante
gráfica de posición–tiempo. de tiempo (figura 9).

Gráfica de aceleración-tiempo (a-t)

De la misma manera como representamos gráficamente en el plano
cartesiano la velocidad y la posición en función del tiempo, podemos
representar la aceleración en una gráfica a-t, para lo cual escribimos en
el eje vertical la aceleración y en el horizontal el tiempo.
Puesto que el movimiento uniformemente variado se produce con
a(m/s) 2 aceleración constante, la gráfica que representa este movimiento es un
segmento de recta horizontal, como el que se observa en la figura 10.

A partir de la ecuación v 5 v 1 a ? t, equivalente a v 2 v 5 at, se ob-
0
0
tiene la variación de la velocidad Dv 5 at, que corresponde al área del
a
rectángulo que se forma entre la recta y el eje horizontal en la gráfica
de a-t (figura 10).
v
Definición
0 t t(s) El área comprendida entre la gráfica de a-t y el eje horizontal representa el
Figura 10. Variación de la velocidad. cambio de velocidad de un objeto.
52 © Santillana

FI10-U2(38-57).indd 52 30/09/10 18:01