Page 69 - Fisica General Burbano

COMPOSICIÓN DE MAS PERPENDICULARES 77

Hemos puesto la misma pulsación w ya que el período de ambos movimientos es el mismo. El
primer movimiento lo consideramos sin corrección de fase por la arbitrariedad en la elección del
origen de tiempos. De la segunda ecuación obtenemos, por desarrollo del seno:
y sen wt cos wt
A 2 = cos j + sen j
y sustituyendo el seno y el coseno de wt por sus valores en función de x:
y x + 1 x 2
A 2 = A 1 cos j - A 1 2 sen j
x cos j
pasando al primer miembro y elevando al cuadrado, se obtiene:
A 1
y 2 x 2 2 2 xy 2 x 2 2
A 2 2 + A 1 2 cos j - AA 2 cos j =sen j - A 1 2 sen j
1
pasando el último término al primer miembro y simplificando:
x 2 y 2 2 xy =sen 2
A 1 2 + A 2 2 - AA 2 cos j j
1
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
ecuación de una elipse, que nos da la forma de la trayectoria en forma implícita.
CASOS PARTICULARES: Fig. IV-13.– Trayectoria de la partí-
1) La diferencia de fase es cero ó 2Kp. La ecuación general queda reducida a: cula sometida a dos MAS perpendicu-
lares y de la misma frecuencia, cuan-
x 2 y 2 2 xy 0 M x L y O P 2 0 y x A 2 x do j =0 ó 2Kp.
A 1 2 + A 2 2 - AA 2 = Þ A 1 N - A 2Q = Þ A 2 = A 1 Þ y = A 1
1
Ecuación de una recta que pasa por el origen de coordenadas y de coeficiente angular positi-
vo. El movimiento es rectilíneo en el primer y tercer cuadrante (Fig. IV-13). La ecuación del movi-
miento vibratorio armónico que resulta para este caso particular es:

r = A 1 2 + A 2 2 sen t w
2) La diferencia de fase es p/2 ó (2K +1) p/2, es decir, los dos movimientos componentes se en-
cuentran en cuadratura. La ecuación general queda reducida a:

x 2 y 2 1 Fig. IV-14.– Trayectoria de la partí-
A 1 2 + A 2 2 = cula sometida a dos MAS perpendicu-
lares y de la misma frecuencia, cuan-
Ecuación de una elipse centrada en los ejes (Fig. IV-14). En este caso, si A =A el movimiento do j =p/2.
1
2
es circular.
3) La diferencia de fase es p ó (2K +1)p. La forma de la ecuación general es:
y 2 x 2 2 xy M y L x O P 2 0 y x A 2 x
A 2 2 + A 1 2 + AA 2 0 = Þ A 2 N + A 1Q = Þ A 2 = - A 1 Þ y = - A 1
1
Ecuación de una recta que pasa por el origen de coordenadas y de coeficiente angular negati-
vo. El movimiento es rectilíneo en el 2.º y 4.º cuadrante (Fig. IV-15).
La ecuación del movimiento vibratorio armónico resultante es:

r = A 1 2 + A 2 2 sen t w
Fig. IV-15.– Trayectoria de la partí-
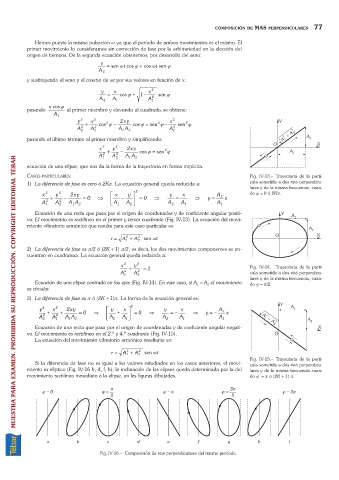
Si la diferencia de fase no es igual a los valores estudiados en los casos anteriores, el movi- cula sometida a dos MAS perpendicu-
miento es elíptico (Fig. IV-16 b, d, f, h); la inclinación de las elipses queda determinada por la del lares y de la misma frecuencia cuan-
movimiento rectilíneo inmediato a la elipse, en las figuras dibujadas. do j =p ó (2K +1) p.

Fig. IV-16.– Composición de MAS perpendiculares del mismo pieríodo.