Page 509 - Fisica General Burbano

ENERGÍA MAGNÉTICA. DESCARGA OSCILANTE DE UN CONDENSADOR 523

Para obtener corrientes oscilantes en un circuito será necesario que la raíz de la ecuación anterior
sea real, es decir:
1 R 2 2 L
CL ³ 4 L 2 Þ R £ C

2
Si suponemos que el circuito no tiene resistencia (R =0): dQ + 1 Q = 0
dt 2 LC
ecuación análoga a la del oscilador armónico (párrafo VI-8), cuya solución, escogiendo conve-
nientemente el origen del tiempo, se podrá escribir:
Q = Q cos 2 pn t
0
y por tanto:
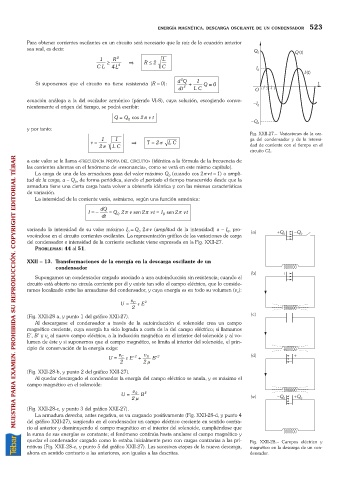
Fig. XXII-27.– Variaciones de la car-
1 1 ga del condensador y de la intensi-
n = Þ T = 2 p L C
2 p LC dad de corriente con el tiempo en el
circuito CL.
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
a este valor se le llama «FRECUENCIA PROPIA DEL CIRCUITO» (idéntica a la fórmula de la frecuencia de
las corrientes alternas en el fenómeno de «resonancia», como se verá en este mismo capítulo).
La carga de una de las armaduras pasa del valor máximo Q (cuando cos 2pnt =1) o ampli-
0
tud de la carga, a – Q , de forma periódica, siendo el período el tiempo transcurrido desde que la
0
armadura tiene una cierta carga hasta volver a obtenerla idéntica y con las mismas características
de variación.
La intensidad de la corriente varía, asimismo, según una función armónica:
dQ
I
I =- = Q 2 pn sen 2 pn t = sen 2 pn t
0
0
dt
variando la intensidad de su valor máximo I =Q 2pn (amplitud de la intensidad) a – I , pro-
0
0
0
vocándose en el circuito corrientes oscilantes. La representación gráfica de las variaciones de carga
del condensador e intensidad de la corriente oscilante viene expresada en la Fig. XXII-27.
PROBLEMAS:44 al 51.
XXII – 13. Transformaciones de la energía en la descarga oscilante de un
condensador
Supongamos un condensador cargado asociado a una autoinducción sin resistencia; cuando el
circuito está abierto no circula corriente por él y existe tan sólo el campo eléctrico, que lo conside-
ramos localizado entre las armaduras del condensador, y cuya energía es en todo su volumen (v ):
c
v 2
U = C e E
2
(Fig. XXII-28 a, y punto 1 del gráfico XXII-27).
Al descargarse el condensador a través de la autoinducción el solenoide crea un campo
magnético creciente, cuya energía ha sido lograda a costa de la del campo eléctrico; si llamamos
E¢, B¢y v al nuevo campo eléctrico, a la inducción magnética en el interior del solenoide y al vo-
s
lumen de éste y si suponemos que el campo magnético, se limita al interior del solenoide, el prin-
cipio de conservación de la energía exige:
v v
2
U = C e E¢ + S B¢ 2
2 2 m
(Fig. XXII-28-b, y punto 2 del gráfico XXII-27).
Al quedar descargado el condensador la energía del campo eléctrico se anula, y es máximo el
campo magnético en el solenoide:
v
U = S B 2
2 m
(Fig. XXII-28-c, y punto 3 del gráfico XXII-27).
La armadura derecha, antes negativa, se va cargando positivamente (Fig. XXII-28-d, y punto 4
del gráfico XXII-27), surgiendo en el condensador un campo eléctrico creciente en sentido contra-
rio al anterior y disminuyendo el campo magnético en el interior del solenoide, cumpliéndose que
la suma de sus energías es constante; el fenómeno continúa hasta anularse el campo magnético y
quedar el condensador cargado como lo estaba inicialmente pero con cargas contrarias a las pri- Fig. XXII-28.– Campos eléctrico y
mitivas (Fig. XXII-28-e, y punto 5 del gráfico XXII-27). Las sucesivas etapas de la nueva descarga, magnético en la descarga de un con-
ahora en sentido contrario a las anteriores, son iguales a las descritas. densador.