Page 225 - Fisica General Burbano

236 EL CAMPO GRAVITATORIO

En efecto; traslademos una partícula de masa m, de un punto a otro infinitamente próximo, situa-
do en la misma superficie equipotencial; el trabajo elemental es: dW =F · dr =mg · dr, y que es:
dW =– mdV =0, puesto que V no varía; por lo tanto: g · dr =gdr cos j =0, y como g ¹0 y
dr ¹0, será cos j =0 y por tanto j =p/2; con lo que queda demostrado que las líneas de fuer-
za y las superficies equipotenciales se cortan perpendicularmente

XI – 10. Movimiento bajo la acción de fuerza gravitatorias
El movimiento de una partícula en el interior de un campo gravitatorio por la acción única de
la fuerza generada en él, es un ejemplo para el que la energía mecánica total y el momento angu-
lar de la partícula respecto al CM del sistema se conservan para cualquiera que sea la distribución
que crea el campo, puesto que éste es conservativo.
En el caso en el que la distribución que genera el campo sea una masa puntual M, (o lo que es
lo mismo, sea una masa esférica que en su exterior produce los mismos efectos que una masa
igual a la de la esfera M colocada en su centro), si es m la masa de la partícula que se mueve en
presencia de M, formando ambas un sistema aislado, A, B, C.... puntos pertenecientes a su trayec-
toria* * (Fig. XI-14), cuyos vectores de posición respecto de O (centro de la esfera) son r , r , r ...,
C
A
B
y en ellos m posee las velocidades v , v , v ..., las magnitudes dinámicas que se conservan por ser
B
C
A
el campo central y por tanto conservativo, son la energía mecánica total y el momento angular res-
pecto de O, pudiéndose escribir para dos puntos cualesquiera (A y B) las ecuaciones:
1 2 GMm 1 2 GMm
E = cte Þ T A +() U A =() T B +( ) U B( ) Þ m v A - = mv B -
2 r A 2 r B
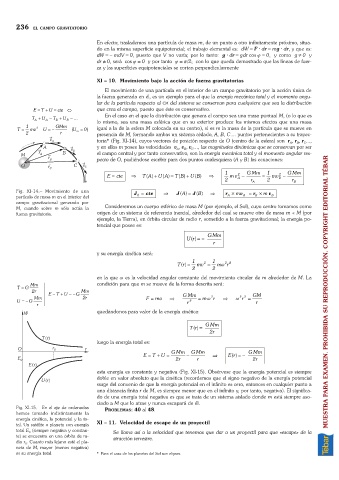
Fig. XI-14.– Movimiento de una J = cte Þ J ()A = J ( )B Þ r ´ m v = r ´m v
partícula de masa m en el interior del 0 A A B B
campo gravitacional generado por
M, cuando sobre m sólo actúa la Consideremos un cuerpo esférico de masa M (por ejemplo, el Sol), cuyo centro tomamos como
fuerza gravitatoria. origen de un sistema de referencia inercial, alrededor del cual se mueve otro de masa m n M (por
ejemplo, la Tierra), en órbita circular de radio r, sometido a la fuerza gravitacional; la energía po-
tencial que posee es:
GMm
Ur () =-
r
y su energía cinética será:
1 2 1 2 2
Tr() = mv = mw r
2 2
en la que w es la velocidad angular constante del movimiento circular de m alrededor de M. La
condición para que m se mueve de la forma descrita será:
GMm 2 2 2 GM MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
F = ma Þ 2 = m w r Þ w r =
r r
quedándonos para valor de la energía cinética:
GMm
Tr() =
2r
luego la energía total es:
GMm G Mm GMm
E = T + U = - Þ Er () = -
2r r 2r
esta energía es constante y negativa (Fig. XI-15). Obsérvese que la energía potencial es siempre
doble en valor absoluto que la cinética (recordemos que el signo negativo de la energía potencial
surge del convenio de que la energía potencial en el infinito es cero, entonces en cualquier punto a
una distancia finita r de M, es siempre menor que en el infinito y, por tanto, negativa). El significa-
do de una energía total negativa es que se trata de un sistema aislado donde m está siempre aso-
ciado a M que lo atrae y nunca escapará de él.
Fig. XI-15.– En el eje de ordenadas PROBLEMAS:40 al 48.
hemos tomado indistintamente la
energía cinética, la potencial y la to- XI – 11. Velocidad de escape de un proyectil
tal. Un satélite o planeta con energía
total E (siempre negativa y constan- Se llama así a la velocidad que tenemos que dar a un proyectil para que «escape» de la
0
te) se encuentra en una órbita de ra- atracción terrestre.
dio r . Cuanto más lejano esté el pla-
0
neta de M, mayor (menos negativa)
es su energía total. * Para el caso de los planetas del Sol son elipses.