Page 79 - Física Tippens: Conceptos y Aplicaciones, Séptima Edición Revisada

60 Capítulo 3 Mediciones técnicas y vectores

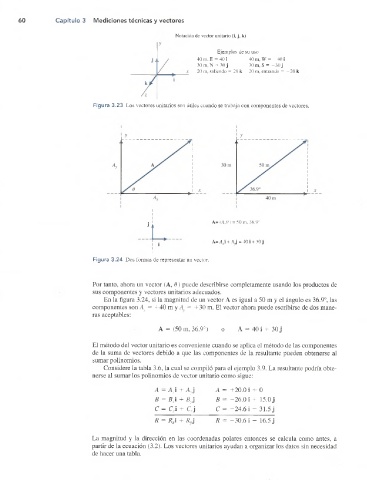
Notación de vector unitario (i, j. k)

Ejemplos de su uso
40 m, E = 40 i 40 m, W = —40 i
30 m, N = 30 j 30 m, S = —30 j
20 m, saliendo = 20 k 20 m, entrando = —20 k

Figura 3.23 Los vectores unitarios son útiles cuando se trabaja con componentes de vectores.

i

i
i
i
= i A= (A,f?) = 50 m, 36.9°
J > V

* j > A= Avi + Avj = 40 i + 30 j
i
i
Figura 3.24 Dos formas de representar un vector.

Por tanto, ahora un vector (A, 9) puede describirse completamente usando los productos de
sus componentes y vectores unitarios adecuados.
En la figura 3.24, si la magnitud de un vector A es igual a 50 m y el ángulo es 36.9°, las
componentes son Ax = +40 m yA = +30 m. El vector ahora puede escribirse de dos mane­
ras aceptables:

A = (50 m, 36.9°) o A = 40i + 30j

El método del vector unitario es conveniente cuando se aplica el método de las componentes
de la suma de vectores debido a que las componentes de la resultante pueden obtenerse al
sumar polinomios.
Considere la tabla 3.6, la cual se compiló para el ejemplo 3.9. La resultante podría obte­
nerse al sumar los polinomios de vector unitario como sigue:

A — Axi + Ayj A = +20.0 i + 0
B = Bxi + Byj B = -26.0 i + 15.0 j
C = Cxi + Cyj C = -24.6 i - 31.5 j

R = Rxi + 7?, j R = -30.6 i - 16.5 j

La magnitud y la dirección en las coordenadas polares entonces se calcula como antes, a
partir de la ecuación (3.2). Los vectores unitarios ayudan a organizar los datos sin necesidad
de hacer una tabla.