Page 519 - Fisica General Burbano

FENÓMENOS DE RESONANCIA 533

das las tensiones e intensidades del circuito; por lo tanto se trabajará con lo que llamaremos el fa-
sor, así por ejemplo, si la intensidad alterna es de la forma I =I (cos wt – j) la escribíamos en for-
0
ma compleja:
[I] =I e i (wt – j)
0
el fasor que le corresponde será: I = I 0 e i j
tendremos que incluir el término e iwt cuando deseemos obtener la expresión específica de la mag-
nitud física.
PROBLEMAS:72 al 79.

H) FENÓMENOS DE RESONANCIA
XXII – 32. Resonancia del circuito básico RLC en serie

«Si en un circuito RLC la reactancia es nula, la intensidad y la FEM están en concordancia
de fase, es decir las dos se anulan o se hacen máximas en el mismo instante (Fig. XXII-33);
y se verifica el fenómeno de RESONANCIA».

En consecuencia: cos j =1
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
1 1
L
X = w - = 0 Þ L w = Þ tg j =0
C w C w
w =1/ LC
y la impedancia Z se hace mínima e igual a R; entonces, I adquiere su mayor valor posible, al ser
0
el denominador de la fórmula (15) mínimo: I =e /R.
0
0
Así, cuando hay concordancia de fase entre la intensidad y la FEM, I crece extraordinariamente
0
haciéndose peligrosa para la seguridad del aislamiento de la línea. Los circuitos industriales no
están preparados para tan altas intensidades por lo que debe evitarse, por tanto, tal fenómeno de
resonancia.
1
Como w =2 pn =2 p/ T, obtenemos: T = =2p L C (FÓRMULA DE THOMSON)*
n
En un circuito RLC resonante, por verificarse Lw =1/Cw, entonces: [V ] =[V ], y el dia-
C
L
grama vectorial será como el de la Fig. XXII-51.
El valor de la frecuencia (w) obtenida para el fenómeno de resonancia en un circuito RLC de Fig. XXII – 51. Diagrama vectorial de
corriente alterna, coincide con la «frecuencia propia» de oscilación de un circuito LC. un circuito RLC en serie y en resonan-
«A tal frecuencia de variación del voltaje, para la cual la corriente del circuito en serie RLC
alcanza su valor máximo, la llamaremos FRECUENCIA NATURAL o PROPIA del circuito (w ) y de-
0
pende únicamente de L y C».
La resonancia eléctrica es análoga a la mecánica, tal y como vimos en el párrafo VII-29. La
energía comunicada al sistema por la fuente es máxima en la resonancia, ya sea ésta eléctrica, la
oscilación de un resorte o se trate de un niño columpiándose, etc.
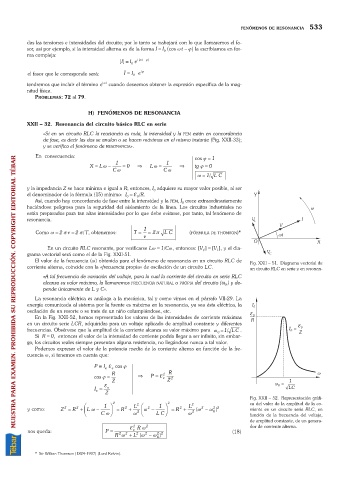
En la Fig. XXII-52, hemos representado los valores de las intensidades de corriente máximas
en un circuito serie LCR, adquiridas para un voltaje aplicado de amplitud constante y diferentes
frecuencias. Obsérvese que la amplitud de la corriente alcanza su valor máximo para w = 1/ LC .
0
Si R =0, entonces el valor de la intensidad de corriente podría llegar a ser infinito, sin embar-
go, los circuitos reales siempre presentan alguna resistencia, no llegándose nunca a tal valor.
Podemos expresar el valor de la potencia media de la corriente alterna en función de la fre-
cuencia w, si tenemos en cuenta que:

I
P = e cos j
e
e
R P= e 2 R
cos j = Z Þ e Z 2
e
I = e
e
Z
Fig. XXII – 52. Representación gráfi-
F 1 I 2 L F 1 I 2 L 2 ca del valor de la amplitud de la co-
2
22
2
y como: Z = R 2 + G H L w - C K J = R 2 + w 2 G H w 2 - LCK J = R 2 + w 2 ( w 2 - w ) rriente en un circuito serie RLC, en
0
w
función de la frecuencia del voltaje,
de amplitud constante, de un genera-
e 2 R w 2 dor de corriente alterna.
nos queda: P = 2 2 e 2 2 22 (18)
R w + L w( -w )
0
* Sir Willian Thomson (1824-1907) (Lord Kelvin).