Page 524 - Fisica General Burbano
P. 524
538 CORRIENTES INDUCIDAS
La suma de las intensidades instantáneas, en un sistema trifásico equilibrado es igual a cero. En
efecto: en un diagrama vectorial las intensidades máximas quedan representadas por vectores
iguales, que forman entre sí ángulos de 2p/3, cuyo resultado es nulo (Fig. XXII-70).
En general se llaman CORRIENTES POLIFÁSICAS, al sistema formado por n corrientes alternas inde-
pendientes, de la misma frecuencia, desfasadas entre cada dos consecutivas en 2p/n. La excepción
a esta definición son las ya vistas corrientes bifásicas, pues para cada una de ellas, el desfase es
2p/4, como en las tetrafásicas pero usando sólo dos corrientes.
Para hacer más económica la instalación para las corrientes trifásicas, vamos a estudiar a con-
tinuación dos sistemas de conexiones de los arrollamientos, que denominaremos en estrella y en
triángulo.
Fig. XXII 66. Conexiones de co- XXII 67. Representación vectorial XXII 68. Alternador trifásico.
rrientes bifásicas. Las flechas indican de las intensidades en corrientes bifá-
el sentido las corrientes en un instan- sicas.
te determinado.
XXII 44. Conexión en estrella y en triángulo
CONEXIÓN EN ESTRELLA: queda representada en la Fig. XXII-71. Los tres circuitos independientes
(abcd, efgh, ijkl) se conectan de forma que sus inducidos tienen un pudo común (P). (Los induci-
dos del alternador están representados por bc, fg y jk).
Las intensidades de corriente de los tres circuitos se anulan, si los circuitos están equilibrados
(Fig. XXII-70). Al no circular corriente por el hilo común (de puntos en la Fig. XXII-71) se puede
eliminar.
«Estando montados en serie cada devanado (be, por ejemplo) con cada línea (ba), la intensi-
dad de fase (intensidad del devanado) y la intensidad de línea o compuesta, son iguales».
TENSIÓN DE FASE es la diferencia de potencial entre los extremos de un devanado: V V =V .
p
bp
b
TENSIÓN COMPUESTA es la diferencia de potencial entre los extremos terminales de dos devanados:
V V =V . Por estar montados en serie los devanados bp y pf se obtiene: MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
f
bf
b
V =(V V ) +(V V ) =(V V ) (V V ) =V V =V cos wt V cos (wt +2 p/3)
p
f
p
f
p
0
0
pb
b
pf
bf
b
p
siendo V la tensión máxima de cada fase.
0
Para realizar la composición geométrica de las dos tensiones, dibujaremos V formando un án-
0
gulo wt con el eje X; otro vector idéntico formando con X un ángulo (w t +2 p/3) (de puntos en la
Fig. XXII-72), del que tomaremos el vector igual y opuesto (signo menos de la fórmula anterior); el
vector resultante de los dos anteriores nos dará la tensión máxima compuesta cuyo valor será, el
doble de la proyección de V sobre la propia resultante:
0
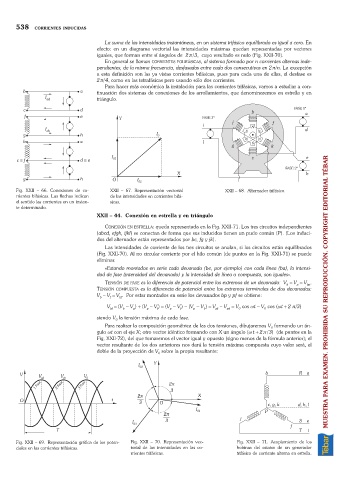
Fig. XXII 69. Representación gráfica de los poten- Fig. XXII 70. Representación vec- Fig. XXII 71. Acoplamiento de los
ciales en las corrientes trifásicas. torial de las intensidades en las co- bobinas del estator de un generador
rrientes trifásicas. trifásico de corriente alterna en estrella.