Page 361 - Fisica General Burbano
P. 361
SUPERPOSICIÓN DE ONDAS. INTERFERENCIAS 373
más sencillo de dos ondas de igual amplitud, viajando en el sentido positivo del eje X (cuerda),
con frecuencias n y n y números de onda k y k . Las funciones de onda respectivas son:
1
2
1
2
y =y sen (w t k x) y =y sen (w t k x)
1
2
2
0
0
2
1
1
y sumando ambas: y =y [sen (w t k x) +sen (w t k x)]
2
0
2
1
1
aplicando de nuevo la expresión (15):
L w k -k O L w k +k O
P
2
2
y = 2 y cos M N w - 1 t - 2 2 1 x sen M N w + 1 t - 2 2 1 x P Q
Q
0
2
2
que, empleando la notación:
k
Dk = k 2 - k 1 k =( k + )/ 2
2
m
1
D =w w 2 -w 1 w m = w( 1 +w )/ 2
2
podemos escribir de la forma:
y = 2 y cos G H 2 w F D t - Dk I K J x sen ( w t -k x )
m
0
m
2
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
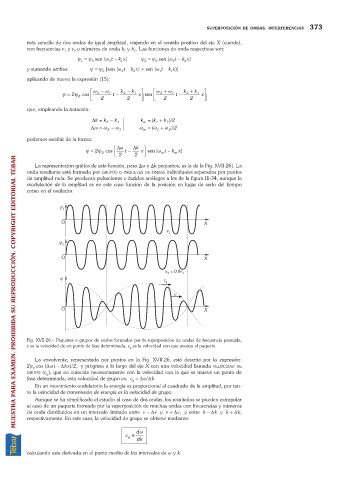
La representación gráfica de esta función, para Dw y Dk pequeños, es la de la Fig. XVII-26). La
onda resultante está formada por GRUPOS o PAQUETES DE ONDAS individuales separados por puntos
de amplitud nula. Se producen pulsaciones o batidos análogos a los de la figura III-34, aunque la
modulación de la amplitud es en este caso función de la posición en lugar de serlo del tiempo
como en el oscilador.
Fig. XVII-26. Paquetes o grupos de ondas formadas por la superposición de ondas de frecuencia parecida,
c es la velocidad de un punto de fase determinada, c es la velocidad con que avanza el paquete.
g
La envolvente, representada por puntos en la Fig. XVII-26, está descrita por la expresión:
2y cos (Dwt Dkx)/2, y progresa a lo largo del eje X con una velocidad llamada VELOCIDAD DE
0
GRUPO (c ), que no coincide necesariamente con la velocidad con la que se mueve un punto de
g
fase determinada; esta velocidad de grupo es: c =Dw/Dk.
g
En un movimiento ondulatorio la energía es proporcional al cuadrado de la amplitud, por tan-
to la velocidad de transmisión de energía es la velocidad de grupo.
Aunque se ha simplificado el estudio al caso de dos ondas, los resultados se pueden extrapolar
al caso de un paquete formado por la superposición de muchas ondas con frecuencias y números
de onda distribuidos en un intervalo limitado entre n Dn y n +Dn, y entre k Dk y k +Dk,
respectivamente. En este caso, la velocidad de grupo se obtiene mediante:
dw
c =
g
dk
calculando esta derivada en el punto medio de los intervalos de w y k.