Page 358 - Fisica General Burbano

370 ONDAS

Fig. XVII-23.– Ondas estacionarias transversales.

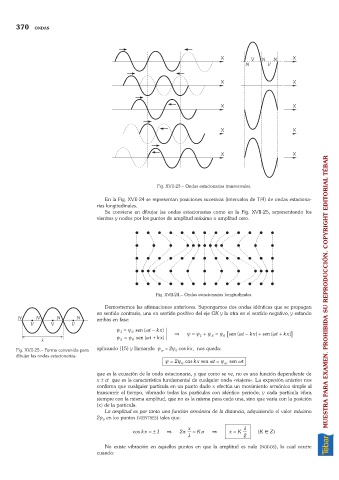
En la Fig. XVII-24 se representan posiciones sucesivas (intervalos de T/4) de ondas estaciona-
rias longitudinales.
Se conviene en dibujar las ondas estacionarias como en la Fig. XVII-25, representando los
vientres y nodos por los puntos de amplitud máxima o amplitud cero.

Fig. XVII-24.– Ondas estacionarias longitudinales. MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR

Demostremos las afirmaciones anteriores. Supongamos dos ondas idénticas que se propagan
en sentido contrario, una en sentido positivo del eje OX y la otra en el sentido negativo, y estando
ambas en fase:

y = y sen ( w -t k ) x Þ y= y + y = y sen ( w - )t kx +sen ( wt + )kx
1
0
y = y sen ( w +t k ) x 1 2 0
2
0
Fig. XVII-25.– Forma convenida para aplicando (15) y llamando y =2y cos kx, nos queda:
or
0
dibujar las ondas estacionarias.
y =2 y cos kx sen w =t y or sen wt
0
que es la ecuación de la onda estacionaria, y que como se ve, no es una función dependiente de
x ±ct que es la característica fundamental de cualquier onda «viajera». La expresión anterior nos
confirma que cualquier partícula en un punto dado x efectúa un movimiento armónico simple al
transcurrir el tiempo, vibrando todas las partículas con idéntico período; y cada partícula vibra
siempre con la misma amplitud, que no es la misma para cada una, sino que varía con la posición
(x) de la partícula.
La amplitud es por tanto una función armónica de la distancia, adquiriendo el valor máximo
2y en los puntos (VIENTRES) tales que:
0
x l
cos kx =±1 Þ 2p = K p Þ x = K (K Î ) Z
l 2
No existe vibración en aquellos puntos en que la amplitud es nula (NODOS), lo cual ocurre
cuando: