Page 378 - Fisica General Burbano

390 ONDAS

unas ondas superficiales en el agua, de las que a simple vista se observa
que su longitud de onda es bastante mayor de 10 cm y que un trozo de
madera que flota en la superficie realiza 120 oscilaciones completas en
un minuto. 2) Tomamos una fotografía de las aguas «rizadas» de un
lago y observamos en ella que entre dos puntos a distancia real de 1 m
hay 20 «rizos» completos. Calcular la velocidad de propagación de tales
rizos. 3) Demostrar que la mínima velocidad de las ondas superficiales
del agua, cuando l es próximo a 10 cm, tiene por valor 23 cm/s.
22. Demostrar que en un sólido las ondas longitudinales viajan a
mayor velocidad que las transversales.
Problema XVII-9. 23. Una cuerda de masa M y longitud l cuelga del techo de una
habitación. 1) Probar que la velocidad de un pulso transversal en fun-
11. Sometemos al extremo de una cuerda a un vibrador que le
produce una onda sinuosidal. Si la ecuación de la vibración en el siste- ción de la posición cuando se propaga a lo largo de ella es c = g , x
ma CGS es: y =5 sen 0,2pt, propagándose en la cuerda con una velo- siendo x la distancia al extremo libre. 2) Probar que un pulso transversal
cidad de 10 cm/s. Determínese la ecuación de la onda producida, y la recorrerá la cuerda en un tiempo 2l /g .
diferencia de fase entre las oscilaciones de dos puntos separados 24. De las funciones que se presentan a continuación, sólo dos
125 cm. pueden representar ecuaciones de onda, de ondas unidimensionales
–2
2
12. Las ecuaciones de dos ondas escritas en el sistema CGS vienen que se propagan en el eje OX: y (x, t) =5 ´10 /[0,25 +(x – 2t) ],
1
–2
2
2
–2
dadas por: y (x, t) =4 sen 2p (4t – 0,5x)y y (x, t) =6 sen (4px – y (x, t) =5 ´10 /[0,25 +(x +4t – 2t)], y (x, t) =5 ´10 /[0,25 +
2
3
2
1
2
– 5pt); calcular en cada caso: 1) Velocidad en función del tiempo, de +(2x +t) ]. 1) Decir cuáles de las funciones: y , y e y son funciones de
2
3
1
un punto situado a 10 cm del origen. 2) Velocidad máxima de ese pun- onda y justificar la contestación. 2) ¿Cuáles son las velocidades de pro-
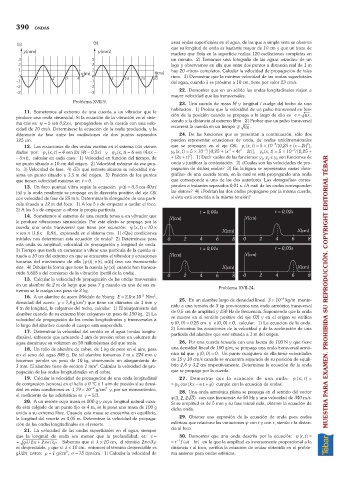
to. 3) Velocidad de fase. 4) ¿En qué instante alcanza su velocidad má- pagación de dichas ondas? 3) En la figura se representan varias «foto-
xima un punto situado a 1,5 m del origen. 5) Posición de los puntos grafías» de una cuerda tensa, en la cual se está propagando una onda
que tienen velocidad máxima en t =0. que corresponde a una de las dos anteriores. Las «fotografías» corres-
13. Un foco puntual vibra según la ecuación y(t) =0,3 cos 40pt ponden a instantes separados 0,01 s. ¿A cuál de las ondas corresponden
(SI) y la onda resultante se propaga en la dirección positiva del eje OX las «fotos»? 4) ¿Podrían las dos ondas propagarse por la misma cuerda,
con velocidad de fase de 25 m/s. Determinar la elongación de una partí- si ésta está sometida a la misma tensión?
cula situada a 12 m del foco: 1) A los 5 s de empezar a oscilar el foco.
2) A los 5 s de empezar a vibrar la propia partícula.
14. Sometemos al extremo de una cuerda tensa a un vibrador que
le produce vibraciones sinusoidales. Por este efecto se propaga por la
cuerda una onda transversal que tiene por ecuación: y(x, t) =10 ´
´sen p (1,6x – 0,8t), expresada en el sistema CGS. 1) ¿Qué condiciones
iniciales nos determinan esta ecuación de onda? 2) Determínese para
esta onda su amplitud, velocidad de propagación y longitud de onda.
3) Tiempo que tarda en comenzar a vibrar una partícula de la cuerda si-
tuada a 10 cm del extremo en que se encuentra el vibrador y ecuaciones
horarias del movimiento de ella [y(t), v(t), a(t)] una vez transcurrido
éste. 4) Dibujar la forma que tiene la cuerda [y(x)] cuando han transcu-
rrido 5,625 s del comienzo de la vibración (perfil de la onda).
15. Calcular la velocidad de propagación de las ondas trasversales
en un alambre de 2 m de largo que pesa 7 g cuando en uno de sus ex- Problema XVII-24.
tremos se le cuelga una pesa de 2 kg. MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
2
16. A un alambre de acero (Módulo de Young: E =2,0 ´10 11 N/m , –2
densidad del acero: r =7,8 g/cm ) que tiene un diámetro de 1 mm y 25. En un alambre largo de densidad lineal 3 ´10 kg/m mante-
3
4 m de longitud, lo colgamos del techo, calcular: 1) El alargamiento del nido a una tensión de 3 kp provocamos una onda armónica transversal
alambre cuando de su extremo libre colgamos un peso de 150 kg. 2) La de 0,5 cm de amplitud y 150 Hz de frecuencia. Suponiendo que la onda
velocidad de propagación de las ondas longitudinales y transversales a se mueve en el sentido positivo del eje OX y en el origen se verifica
lo largo del alambre cuando el cuerpo está suspendido. y(0, 0) =0,25 cm y v(0, 0) <0, calcular: 1) La ecuación de la onda.
17. Determinar la velocidad del sonido en el agua (ondas longitu- 2) Encontrar las ecuaciones de la velocidad y de la aceleración de una
dinales), sabiendo que actuando 1 atm de presión sobre un volumen de partícula del alambre que esté situada a 1 m del origen.
agua disminuye su volumen en 50 millonésimas del que tenía. 26. Por una cuerda tensada con una fuerza de 100 N y que tiene
18. Un rollo de alambre de cobre, de 1 kg de peso en el aire, pesa una densidad lineal de 100 g/m, se propaga una onda transversal armó-
en el seno del agua 886 g. De tal alambre tomamos 1 m y 224 mm y nica tal que y(0, 0) =0. Un punto cualquiera de ella tiene velocidades
hacemos pender un peso de 10 kg, observando un alargamiento de de 15 y 10 cm/s cuando se encuentra separado de su posición de equili-
1 mm. El alambre tiene de sección 1 mm . Calcular la velocidad de pro- brio 2,8 y 3,2 cm respectivamente. Determinar la ecuación de la onda
2
pagación de las ondas longitudinales en el cobre. que se propaga por la cuerda.
19. Calcular la velocidad de propagación de una onda longitudinal 27. Demostrar que la ecuación de una onda: y (x, t) =
de compresión (sonora) en el helio a 0 °C y 1 atm de presión si su densi- =y cos (kx – w t +j) cumple con la ecuación de ondas.
0
dad en estas condiciones es 1,79 ´10 –4 g/cm y, por ser monoatómico, 28. Una onda armónica plana se propaga en el sentido del vector
3
el coeficiente de las adiabáticas es g =5/3. v (, ,32 2 3 ) con una frecuencia de 50 Hz y una velocidad de 340 m/s.
20. A un resorte cuya masa es 200 g y cuya longitud natural cuan- Si su amplitud es de 5 mm y su fase inicial nula, obtener la ecuación de
do está colgado de un punto fijo es 4 m, se le pone una masa de 100 g dicha onda.
unida a su extremo libre. Cuando esta masa se encuentra en equilibrio,
la longitud del resorte es 4,05 m. Determinar la velocidad de propaga- 29. Obtener una expresión de la ecuación de onda para ondas
ción de las ondas longitudinales en el resorte. esféricas que relacione las variaciones y con t y con r, siendo r la distan-
21. La velocidad de las ondas superficiales en el agua, siempre cia al foco.
que la longitud de onda sea menor que la profundidad, es: c = 30. Demostrar que una onda descrita por la ecuación: y(r, t) =
– 1
/
= g l / 2p +2ps l r . Sabemos que si l >10 cm, el término 2ps/lr =r f (wt – kr) en la que la amplitud es inversamente proporcional a la
es despreciable, y que si l <10 cm, entonces el término despreciable es distancia r al foco, verifica la ecuación de ondas obtenida en el proble-
3
gl/2p. DATOS: r =1 g/cm , s =75 dyn/cm. 1) Calcular la velocidad de ma anterior para ondas esféricas.