Page 335 - Fisica General Burbano

346 PRIMER Y SEGUNDO PRINCIPIOS DE LA TERMODINÁMICA

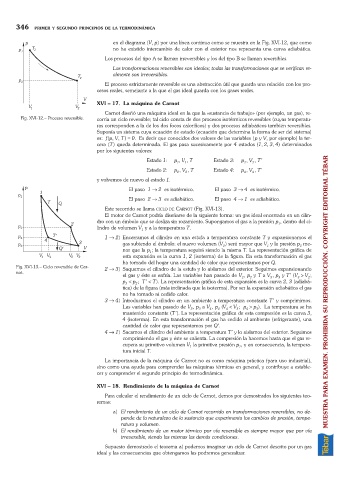
en el diagrama (V, p) por una línea continua como se muestra en la Fig. XVI-12, que como
no ha existido intercambio de calor con el exterior nos representa una curva adiabática.
Los procesos del tipo A se llaman irreversibles y los del tipo B se llaman reversibles.
Las transformaciones reversibles son ideales; todas las transformaciones que se verifican re-
almente son irreversibles.
El proceso estrictamente reversible es una abstracción útil que guarda una relación con los pro-
cesos reales, semejante a la que el gas ideal guarda con los gases reales.

XVI – 17. La máquina de Carnot
Carnot diseñó una máquina ideal en la que la «sustancia de trabajo» (por ejemplo, un gas), re-
Fig. XVI-12.– Proceso reversible. corría un ciclo reversible; tal ciclo consta de dos procesos isotérmicos reversibles (cuyas temperatu-
ras corresponden a la de los dos focos caloríficos) y dos procesos adiabáticos también reversibles.
Suponía un sistema cuya ecuación de estado (ecuación que determina la forma de ser del sistema)
es: f(p, V, T) =0. Es decir que conocidos dos valores de las variables (p y V, por ejemplo) la ter-
cera (T) queda determinada. El gas pasa sucesivamente por 4 estados (1, 2, 3, 4) determinados
por los siguientes valores:
Estado 1: p , V , T Estado 3: p , V , T¢
3
1
3
1
Estado 2: p , V , T Estado 4: p , V , T¢
2
4
2
4
y volvemos de nuevo al estado 1.
El paso 1 ® 2 es isotérmico. El paso 3 ® 4 es isotérmico.
El paso 2 ® 3 es adiabático. El paso 4 ® 1 es adiabático.
Este recorrido se llama CICLO DE CARNOT (Fig. XVI-13).
El motor de Carnot podría diseñarse de la siguiente forma: un gas ideal encerrado en un cilin-
dro con un émbolo que se desliza sin rozamiento. Supongamos el gas a la presión p , dentro del ci-
1
lindro de volumen V y a la temperatura T.
1
1 ® 2) Encerramos el cilindro en una estufa a temperatura constante T y expansionamos el
gas subiendo el émbolo: el nuevo volumen (V ) será mayor que V y la presión p me-
2
2
1
nor que la p ; la temperatura seguirá siendo la misma T. La representación gráfica de
1
esta expansión es la curva 1, 2 (isoterma) de la figura. En esta transformación el gas
ha tomado del hogar una cantidad de calor que representamos por Q.
Fig. XVI-13.– Ciclo reversible de Car- 2 ® 3) Saquemos el cilindro de la estufa y lo aislamos del exterior. Seguimos expansionando
not.
el gas y éste se enfría. Las variables han pasado de V , p y T a V , p y T¢(V >V ;
2
3
2
2
3
3
p <p ; T¢<T). La representación gráfica de esta expansión es la curva 2, 3 (adiabá-
2
3
tica) de la figura (más inclinada que la isoterma). Por ser la expansión adiabática el gas
no ha tomado ni cedido calor. MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
3 ® 4) Introducimos el cilindro en un ambiente a temperatura constante T¢y comprimimos.
Las variables han pasado de V , p a V , p (V <V ; p >p ). La temperatura se ha
3
4
4
3
3
4
4
3
mantenido constante (T¢). La representación gráfica de esta compresión es la curva 3,
4 (isoterma). En esta transformación el gas ha cedido al ambiente (refrigerante), una
cantidad de calor que representamos por Q¢.
4 ® 1) Sacamos el cilindro del ambiente a temperatura T¢y lo aislamos del exterior. Seguimos
comprimiendo el gas y éste se calienta. La compresión la hacemos hasta que el gas re-
cupera su primitivo volumen V la primitiva presión p , y en consecuencia, la tempera-
1
1
tura inicial T.
La importancia de la máquina de Carnot no es como máquina práctica (para uso industrial),
sino como una ayuda para comprender las máquinas térmicas en general, y contribuye a estable-
cer y comprender el segundo principio de termodinámica.
XVI – 18. Rendimiento de la máquina de Carnot
Para calcular el rendimiento de un ciclo de Carnot, demos por demostrados los siguientes teo-
remas:
a) El rendimiento de un ciclo de Carnot recorrido en transformaciones reversibles, no de-
pende de la naturaleza de la sustancia que experimenta los cambios de presión, tempe-
ratura y volumen.
b) El rendimiento de un motor térmico por vía reversible es siempre mayor que por vía
irreversible, siendo las mismas las demás condiciones.
Supuesto demostrado el teorema a) podemos imaginar un ciclo de Carnot descrito por un gas
ideal y las consecuencias que obtengamos las podremos generalizar.