Page 246 - Fisica General Burbano

HIDROSTÁTICA 257

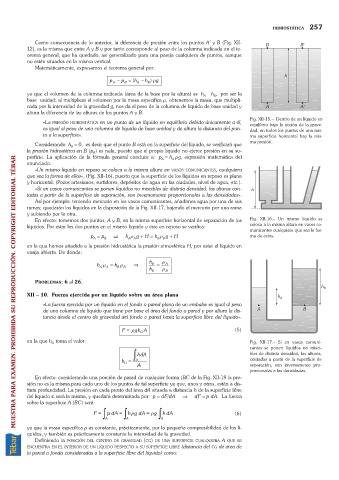
Como consecuencia de lo anterior, la diferencia de presión entre los puntos A¢y B (Fig. XII-
12), es la misma que entre A y B y por tanto corresponde al peso de la columna indicada en el te-
orema general, que ha quedado, así generalizado para una pareja cualquiera de puntos, aunque
no estén situados en la misma vertical.
Matemáticamente, expresamos el teorema general por:

p - p B =( h A h - ) r g
B
A
ya que el volumen de la columna indicada (área de la base por la altura) es h – h , por ser la
A
B
base unidad; al multiplicar el volumen por la masa específica r, obtenemos la masa, que multipli-
cada por la intensidad de la gravedad g, nos da el peso de la columna de líquido de base unidad y
altura la diferencia de las alturas de los puntos A y B.
Fig. XII-15.– Dentro de un líquido en
«La PRESIÓN HIDROSTÁTICA en un punto de un líquido en equilibrio debida únicamente a él, equilibrio bajo la acción de la grave-
es igual al peso de una columna de líquido de base unidad y de altura la distancia del pun- dad, en todos los puntos de una mis-
to a la superficie». ma superficie horizontal hay la mis-
ma presión.
Considerando h =0, es decir que el punto B está en la superficie del líquido, se verificará que
B
la presión hidrostática en B (p ) es nula, puesto que el propio líquido no ejerce presión en su su-
B
perficie. La aplicación de la fórmula general conduce a: p =h rg, expresión matemática del
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
A
A
enunciado.
«Un mismo líquido en reposo se coloca a la misma altura en VASOS COMUNICANTES, cualquiera
que sea la forma de ellos», (Fig. XII-16), puesto que la superficie de los líquidos en reposo es plana
y horizontal. (Pozos artesianos, surtidores, depósitos de agua en las ciudades, nivel de agua, etc.).
«Si en vasos comunicantes se ponen líquidos no miscibles de distinta densidad, las alturas con-
tadas a partir de la superficie de separación, son inversamente proporcionales a las densidades».
Así por ejemplo: teniendo mercurio en los vasos comunicantes, añadimos agua por una de sus
ramas; quedarán los líquidos en la disposición de la Fig. XII-17, bajando el mercurio por una rama
y subiendo por la otra.
En efecto: tomemos dos puntos, A y B, en la misma superficie horizontal de separación de los Fig. XII-16.– Un mismo líquido se
líquidos. Por estar los dos puntos en el mismo líquido y éste en reposo se verifica: coloca a la misma altura en vasos co-
municantes cualquiera que sea la for-
p =p B Þ h r g +H =h r g +H ma de éstos.
B
B
A
A
A
en la que hemos añadido a la presión hidrostática la presión atmosférica H, por estar el líquido en
vasija abierta. De donde:
h B r A
h r = h r B Þ h B = r B
A
B
A
PROBLEMAS:6 al 26.
XII – 10. Fuerza ejercida por un líquido sobre un área plana
«La fuerza ejercida por un líquido en el fondo o pared plana de un embalse es igual al peso
de una columna de líquido que tiene por base el área del fondo o pared y por altura la dis-
tancia desde el centro de gravedad del fondo o pared hasta la superficie libre del líquido».

F = r gh A (5)
G
en la que h toma el valor: Fig. XII-17.– Si en vasos comuni-
z hdA cantes se ponen líquidos no misci-
G
bles de distinta densidad, las alturas,
h = A A contadas a partir de la superficie de
G
separación, son inversamente pro-
porcionales a las densidades.
En efecto: considerando una porción de pared de cualquier forma (BC de la Fig. XII-18 la pre-
sión no es la misma para cada uno de los puntos de tal superficie ya que, unos y otros, están a dis-
tinta profundidad. La presión en cada punto del área dA situada a distancia h de la superficie libre
del líquido si será la misma, y quedará determinada por: p =dF/dA Þ dF =pdA. La fuerza
sobre la superficie A (BC) será:
F = zz A h g dA =r r g z A h dA (6)
p dA =
A
ya que la masa específica r es constante, prácticamente, por la pequeña compresibilidad de los lí-
quidos, y también es prácticamente constante la intensidad de la gravedad.
Definiendo la POSICIÓN DEL CENTRO DE GRAVEDAD (CG) DE UNA SUPERFICIE CUALQUIERA A QUE SE
ENCUENTRA EN EL INTERIOR DE UN LÍQUIDO RESPECTO A SU SUPERFICIE LIBRE (distancia del CG de área de
la pared o fondo considerados a la superficie libre del líquido) como: