Page 243 - Fisica General Burbano

254 ESTUDIO BÁSICO DE LA ESTRUCTURA DE LA MATERIA. MECÁNICA DE FLUIDOS

dF =– p dA cos a dF =– p dA cos b dF =– p dA cos g
z
y
x
donde a, b y g son los ángulos que forma la normal a la superficie dA con los ejes.
La fuerza ejercida sobre la cara OBC de área dA será p dA , siendo p la presión sobre di-
1
1
1
1
cha cara, y es paralela al eje OX; la fuerza ejercida sobre OAC será p dA paralela al eje OY y so-
2
2
bre OAB actuará p dA paralela al eje OZ.
3
3
Al encontrarse el tetraedro en equilibrio, la resultante de todas las fuerzas que actúan sobre él
tendrá que ser nula y considerando despreciables las fuerzas gravitacionales, obtenemos:
– p dA cos a +p dA =0 – pdA cos b +p dA =0 – p dA cos g +p dA =0 (1)
3
3
2
2
1
1
y como dA , dA y dA son las proyecciones de dA, resulta:
1
2
3
dA =dA cos a dA =dA cos b dA =dA cos g
2
1
3
Fig. XII-9.– Para demostrar que la sustituyendo en (1) se obtiene:
presión es una magnitud escalar.
p =p =p =p 3
2
1
obsérvese que el error cometido al despreciar las fuerzas de gravitación va disminuyendo a medi-
da que O se aproxima a P, y en el límite no existe error alguno, y como las cuatro presiones ejerci-
das sobre elementos de superficie distintamente orientados y que pasan por P son iguales, queda
demostrado el carácter escalar de la presión.
Sin embargo la fuerza debida a la presión es una magnitud vectorial, cuya dirección es perpen-
dicular a la superficie sobre la que actúa, y de sentido hacia el interior del cuerpo al que pertenece
la superficie. En la ecuación: dF =pdA el factor que hace vector al segundo miembro es la super-
ficie, la cual, en este caso, se representa por un vector, perpendicular al elemento de superficie, y
cuyo módulo es la medida de la superficie. Así escribiremos:
dF = p dA = p dA n
siendo n el vector unitario en la dirección indicada.
XII – 7. Hipótesis y definiciones
Para realizar el estudio de líquidos y gases nos imaginamos un modelo al que llamaremos
FLUIDOS PERFECTOS, en el que las fuerzas de cohesión las consideramos nulas y no tenemos
en cuenta el movimiento térmico de sus partículas en su interior, en ellos «una de sus partes
se puede desplazar en su propio seno, sin efectuar esfuerzo ni trabajo alguno, contra las
fuerzas de cohesión». (CONDICIÓN DE PERFECTA MOVILIDAD).
El estudio de los líquidos en equilibrio constituye la HIDROSTÁTICA. Los LÍQUIDOS son cuerpos
que tienen volumen determinado y adoptan la forma de la vasija que los contiene.
Fig. XII-10.– Forma adoptada por Consideraremos a los líquidos perfectos como incompresibles: ejerciendo compresiones sobre
los perdigones contenidos dentro de ellos, su volumen permanece constante. (En realidad los líquidos no gozan de la perfecta movili-
un cilindro que gira alrededor de su dad ni de la incompresibilidad). MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
eje con velocidad angular constante.
«Diremos que un líquido está en EQUILIBRIO cuando no existe movimiento relativo entre las
partículas que lo componen».
Así por ejemplo, son casos de equilibrio relativo, un líquido contenido en un recipiente cilíndri-
co girando alrededor de su eje de simetría con velocidad angular constante, un líquido en el inte-
rior de una cisterna sometido a una aceleración rectilínea constante; un líquido en REPOSO (en un
sistema inercial) es también un caso particular de equilibrio.
Para comprender la idea de líquido en equilibrio relativo, analicemos el caso, que consideramos
similar, de unos perdigones contenidos dentro de un cilindro que gira alrededor de su eje de si-
metría con velocidad angular constante; los perdigones adoptan la forma indicada en la Fig. XII-10,
en posiciones que no varían con relación a los demás (no existe movimiento relativo de unos per-
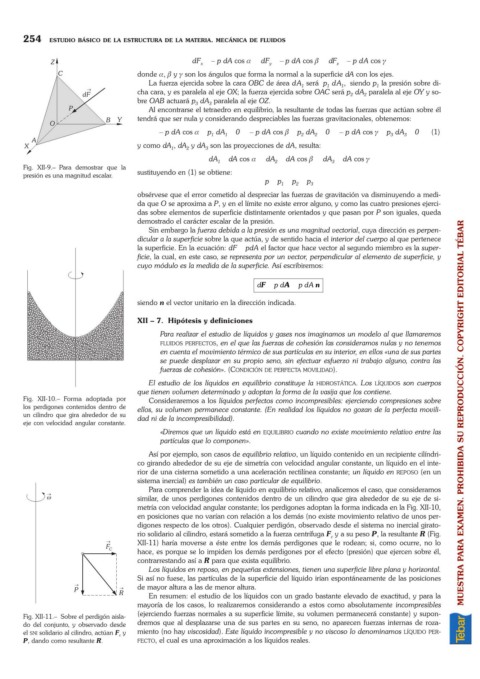
digones respecto de los otros). Cualquier perdigón, observado desde el sistema no inercial girato-
rio solidario al cilindro, estará sometido a la fuerza centrífuga F y a su peso P, la resultante R (Fig.
c
XII-11) haría moverse a éste entre los demás perdigones que le rodean; si, como ocurre, no lo
hace, es porque se lo impiden los demás perdigones por el efecto (presión) que ejercen sobre él,
contrarrestando así a R para que exista equilibrio.
Los líquidos en reposo, en pequeñas extensiones, tienen una superficie libre plana y horizontal.
Si así no fuese, las partículas de la superficie del líquido irían espontáneamente de las posiciones
de mayor altura a las de menor altura.
En resumen: el estudio de los líquidos con un grado bastante elevado de exactitud, y para la
mayoría de los casos, lo realizaremos considerando a estos como absolutamente incompresibles
Fig. XII-11.– Sobre el perdigón aisla- (ejerciendo fuerzas normales a su superficie límite, su volumen permanecerá constante) y supon-
do del conjunto, y observado desde dremos que al desplazarse una de sus partes en su seno, no aparecen fuerzas internas de roza-
el SNI solidario al cilindro, actúan F y miento (no hay viscosidad). Este líquido incompresible y no viscoso lo denominamos LÍQUIDO PER-
c
P, dando como resultante R. FECTO, el cual es una aproximación a los líquidos reales.