Page 681 - Fisica General Burbano

700 CORTEZA ATÓMICA

Si hacemos la sustitución e i ± a = cos a i ± sen a , el corchete de la expresión anterior se trans-
forma en:
F cos G Et EtI F cos G E t EtI
J
1
1
H h + i sen h K H h - i sen h K J +
2
2
+G F H cos Et i - sen EtI F cos G E t + i sen EtI J = 2 cos (E - h E 1 ) t
J
h K
2
2
1
h K H
1
2
h
h
2
2
y en definitiva: Y (, )x t 2 = A y 2 ( )x + A y 2 ( )x + 2 A A y ( )x y ( ) cosx (E - E 1 ) t
2
2
1
2
1
2
1
1
2
h
Según esta expresión, durante la transición del estado excitado 2 al estado 1, la densidad de
probabilidad y, por tanto, la densidad de carga tiene un término que oscila con una frecuencia:
E - E E - E
n = 2 1 = 2 1
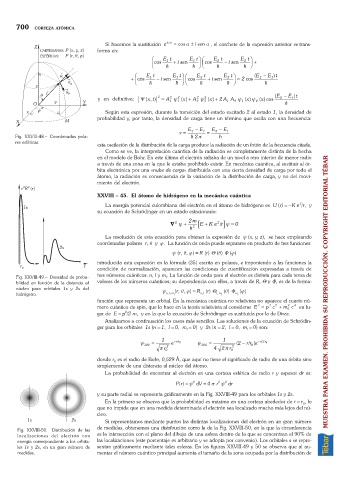
Fig. XXVIII-48.– Coordenadas pola- h 2 p h
res esféricas.
esta oscilación de la distribución de la carga produce la radiación de un fotón de la frecuencia citada.
Como se ve, la interpretación cuántica de la radiación es completamente distinta de la hecha
en el modelo de Bohr. En este último el electrón saltaba de un nivel a otro interior de menor radio
a través de una zona en la que le estaba prohibido existir. En mecánica cuántica, al sustituir al ór-
bita electrónica por una «nube de carga» distribuida con una cierta densidad de carga por todo el
átomo, la radiación es consecuencia de la variación de la distribución de carga, y no del movi-
miento del electrón.
XXVIII – 45. El átomo de hidrógeno en la mecánica cuántica
2
La energía potencial culombiana del electrón en el átomo de hidrógeno es U (r) =–Ke /r,y
su ecuación de Schrödinger en un estado estacionario:
2 m
2 2
Ñ Ñ y + 2 E +K e r/ y = 0
h
La resolución de esta ecuación para obtener la expresión de y (x, y, z), se hace empleando
coordenadas polares r, q y j. La función de onda puede separarse en producto de tres funciones:
y (r, q, j) =R (r) Q (q) F (j)
introducida esta expresión en la fórmula (35) escrita en polares, e imponiendo a las funciones la
condición de normalización, aparecen las condiciones de cuantificación expresadas a través de
Fig. XXVIII-49.– Densidad de proba- tres números cuánticos: n, l y m. La función de onda para el electrón es distinta para cada terna de
l
bilidad en función de la distancia al valores de los números cuánticos; su dependencia con ellos, a través de R, Q y F, es de la forma:
núcleo para orbitales 1s y 2s del y (r, q, j) =R (r) Q (q) F (j)
hidrógeno. n, l, m l n,l l, m l m l MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
función que representa un orbital. En la mecánica cuántica no relativista no aparece el cuarto nú-
2 2 2 2 4
mero cuántico de spin, que lo hace en la teoría relativista al considerar E = p c + m c en lu-
0
gar de E =p /2m, y en la que la ecuación de Schrödinger es sustituida por la de Dirac.
2
Analizamos a continuación los casos más sencillos. Las soluciones de la ecuación de Schrödin-
ger para los orbitales 1s (n =1, l =0, m =0)y 2s(n =2, l =0, m =0) son:
l
l
1 1
/
y 100 = e -rr/ 0 y 200 = ( 2 - rr e ) -r/ 2 0 r
0
p r 0 3 4 2 p r 0 3
donde r es el radio de Bohr, 0,529 Å, que aquí no tiene el significado de radio de una órbita sino
0
simplemente de una distancia al núcleo del átomo.
La probabilidad de encontrar al electrón en una corteza esférica de radio r y espesor dr es:
2
2
P(r) =y dV =4 p r y dr
2
y su parte radial se representa gráficamente en la Fig. XXVIII-49 para los orbitales 1s y 2s.
En la primera se observa que la probabilidad es máxima en una corteza alrededor de r =r , lo
0
que no impide que en una medida determinada el electrón sea localizado mucho más lejos del nú-
cleo.
Si representamos mediante puntos las distintas localizaciones del electrón en un gran número
Fig. XXVIII-50.– Distribución de las de medidas, obtenemos una distribución como la de la Fig. XXVIII-50, en la que la circunferencia
localizaciones del electrón con es la intersección con el plano del dibujo de una esfera dentro de la que se concentran el 90% de
energía correspondiente a los orbita- las localizaciones (este porcentaje es arbitrario y se adopta por convenio). Los orbitales s se repre-
les 1s y 2s, en un gran número de sentan gráficamente mediante tales esferas. En las figuras XXVIII-49 y 50 se observa que al au-
medidas. mentar el número cuántico principal aumenta el tamaño de la zona ocupada por la distribución de