Page 466 - Fisica General Burbano
P. 466
480 EL CAMPO MAGNÉTICO
hacia abajo que desequilibra la balanza. Para conseguir un nuevo equilibrio es necesario quitar del
platillo pesas; este peso (Mg), nos mide la fuerza que actúa sobre el hilo. Tal fuerza tiene por valor,
según la (3): Mg =BIl en la que la longitud EF =l, y sen j =1. El valor de B es: B =Mg/Il.
PROBLEMA:6.
XXI 7. Acción de un campo magnético sobre un circuito. Momento magnético de
una espira
«Un circuito plano se orienta en un campo magnético perpendicularmente a las líneas de
campo, de forma que éstas entran por su cara S y le salen por la N».
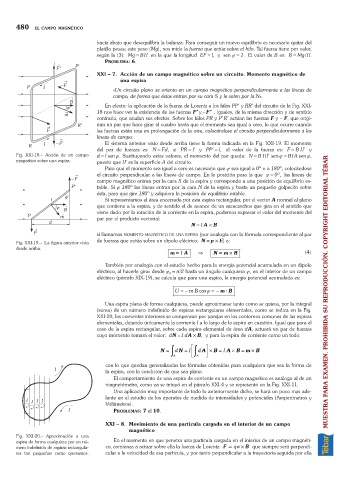
En efecto: la aplicación de la fuerza de Lorentz a los hilos PP¢y RR¢del circuito de la Fig. XXI-
18 nos hace ver la existencia de las fuerzas F¢¢y F¢¢, iguales, de la misma dirección y de sentido
contrario, que anulan sus efectos. Sobre los hilos PR y P¢R¢actúan las fuerzas F y F, que origi-
nan un par que hace girar al cuadro hasta que el momento sea igual a cero, lo que ocurre cuando
las fuerzas están una en prolongación de la otra, colocándose el circuito perpendicularmente a las
líneas de campo.
El sistema anterior visto desde arriba tiene la forma indicada en la Fig. XXI-19. El momento
del par de fuerzas es: N =Fd,si PR =l¢ y PP¢=l, el valor de la fuerza es: F =BIl¢ y
Fig. XXI-18. Acción de un campo d =l sen j. Sustituyendo estos valores, el momento del par queda: N =BIll¢sen j =BIA sen j,
magnético sobre una espira. puesto que ll¢es la superficie A del circuito.
Para que el momento sea igual a cero es necesario que j sea igual a 0º o a 180º, colocándose
el circuito perpendicular a las líneas de campo. En la posición para la que j =0º, las líneas de
campo magnético entran por la cara S de la espira y corresponde a una posición de equilibrio es-
table. Si j 180º las líneas entran por la cara N de la espira y basta un pequeño golpecito sobre
ésta, para que gire 180º y adquiera la posición de equilibrio estable.
Si representamos al área encerrada por esta espira rectangular, por el vector A normal al plano
que contiene a la espira, y de sentido el de avance de un sacacorchos que gira en el sentido que
viene dado por la rotación de la corriente en la espira, podemos expresar el valor del momento del
par por el producto vectorial:
N =I A ´B
si llamamos MOMENTO MAGNÉTICO DE UNA ESPIRA (por analogía con la fórmula correspondiente al par
de fuerzas que actúa sobre un dipolo eléctrico: N =p ´E)a:
Fig. XXI-19. La figura anterior vista
desde arriba.
m = I A Þ N = m ´ B (4)
También por analogía con el estudio hecho para la energía potencial acumulada en un dipolo
eléctrico, al hacerle girar desde j =p/2 hasta un ángulo cualquiera j, en el interior de un campo
0
eléctrico (párrafo XIX-19), se calcula que para una espira, la energía potencial acumulada es:
U =- m B cos j = -mB? MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
Una espira plana de forma cualquiera, puede aproximarse tanto como se quiera, por la integral
(suma) de un número indefinido de espiras rectangulares elementales, como se indica en la Fig.
XXI-20; las corrientes interiores se compensan por parejas en los contornos comunes de las espiras
elementales, dejando únicamente la corriente I a lo largo de la espira en cuestión. Igual que para el
caso de la espira rectangular, sobre cada espira elemental de área dA, actuará un par de fuerzas
cuyo momento tomará el valor: dN =IdA ´B, y para la espira de corriente como un todo:
zz O
L
P
N = d N =I M N A d A ´ B =I A ´ B = m B ´
Q
A
con lo que quedan generalizadas las fórmulas obtenidas para cualquiera que sea la forma de
la espira, con la condición de que sea plana.
El comportamiento de una espira de corriente en un campo magnético es análogo al de un
magnetómetro, como ya se intuyó en el párrafo XXI-4 y se representó en la Fig. XXI-11.
Una aplicación muy importante de todo lo anteriormente dicho, se hará un poco mas ade-
lante en el estudio de los aparatos de medida de intensidades y potenciales (Amperímetros y
Voltímetros).
PROBLEMAS:7 al 10.
XXI 8. Movimiento de una partícula cargada en el interior de un campo
magnético
Fig. XXI-20. Aproximación a una
espira de forma cualquiera por un nú- En el momento en que penetra una partícula cargada en el interior de un campo magnéti-
mero indefinido de espiras rectangula- co, comienza a actuar sobre ella la fuerza de Lorentz: F = qv ´B que siempre será perpendi-
res tan pequeñas como queramos. cular a la velocidad de esa partícula, y por tanto perpendicular a la trayectoria seguida por ella