Page 344 - Fisica General Burbano

PROBLEMAS 355

funciona como frigorífico (recorrido a la inversa) y recibe 2 000 calorías verso, en la unidad de tiempo. 3) Sacar consecuencias acerca de la re-
del foco a 273 K. Calcular la eficiencia. 4) Cuántas calorías cede al foco versibilidad o irreversibilidad del proceso.
caliente. 41. ¿Qué cantidad de calor hace falta para duplicar la temperatura
33. 1) Una bomba de calor que funciona con un motor de Carnot en una transformación cuariestática isocora de 100 l de hidrógeno a
por vía reversible mantiene una habitación a 21 °C, extrayendo calor del 3 atm de presión y 300 K de temperatura? Calcúlese la variación de en-
exterior que se encuentra a 11 °C. Si para ello hay que aportar tropía en la transformación. Considérese al gas como ideal.
3,8 kcal/s a la habitación y el kW · h cuesta 10 céntimos de euro, de- 42. Se realiza una transformación cuasiestática isoterma en un gas
terminar el gasto diario. 2) En verano el exterior se encuentra a 30 °C y ideal, desde un volumen de 10 l, presión de 5 atm a la temperatura de
sacamos 4 kcal/s de la habitación, con el mismo gasto que en invierno; 300 K hasta que se reduce el volumen a la mitad. Calcular: 1) La pre-
determinar la temperatura que conseguimos en la habitación. sión final del gas. 2) Número de moles. 3) Trabajo y calor en la trans-
34. A un resorte, cuya longitud natural, cuando está colgado de un formación. 4) Variación de entropía en la transformación.
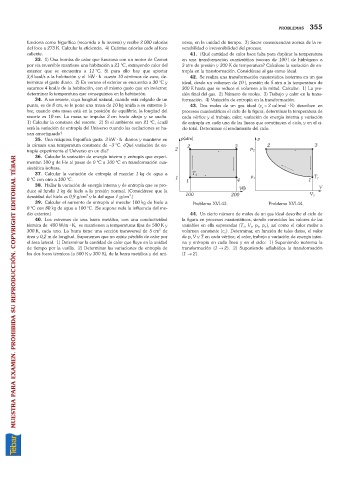
punto, es de 8 cm, se le pone una masa de 10 kg unida a su extremo li- 43. Dos moles de un gas ideal (c =3 cal/mol · K) describen en
v
bre; cuando esta masa está en la posición de equilibrio, la longitud del procesos cuasiestáticos el ciclo de la figura; determinar la temperatura de
resorte es 10 cm. La masa se impulsa 3 cm hacia abajo y se suelta. cada vértice y el trabajo, calor, variación de energía interna y variación
1) Calcular la constane del resorte. 2) Si el ambiente son 21 °C, ¿cuál de entropía en cada una de las líneas que constituyen el ciclo, y en el ci-
será la variación de entropía del Universo cuando las oscilaciones se ha- clo total. Determinar el rendimiento del ciclo.
yan amortiguado?
35. Una máquina frigorífica gasta 3 kW · h diarios y mantiene en
la cámara una temperatura constante de –3 °C. ¿Qué variación de en-
tropía experimenta el Universo en un día?
36. Calcular la variación de energía interna y entropía que experi-
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
mentan 100 g de He al pasar de 0 °C a 100 °C en transformación cua-
siestática isobara.
37. Calcular la variación de entropía al mezclar 1 kg de agua a
0 °C con otro a 100 °C.
38. Hallar la variación de energía interna y de entropía que se pro-
duce al fundir 1 kg de hielo a la presión normal. (Considérese que la
3
3
densidad del hielo es 0,9 g/cm y la del agua 1 g/cm .)
39. Calcular el aumento de entropía al mezclar 100 kg de hielo a Problema XVI-43. Problema XVI-44.
0 °C con 80 kg de agua a 100 °C. (Se supone nula la influencia del me-
dio exterior.) 44. Un cierto número de moles de un gas ideal describe el ciclo de
40. Los extremos de una barra metálica, con una conductividad la figura en procesos cuasiestáticos, siendo conocidos los valores de las
térmica de 400 W/m · K, se mantienen a temperaturas fijas de 500 K y variables en ella expresadas (T , V , p , p ), así como el calor molar a
1
1
2
1
2
300 K, cada uno. La barra tiene una sección transversal de 5 cm de volumen constante (c ). Determinar, en función de tales datos, el valor
v
área y 0,2 m de longitud. Suponemos que no existe pérdida de calor por de p, V y T en cada vértice; el calor, trabajo y variación de energía inter-
el área lateral. 1) Determinar la cantidad de calor que fluye en la unidad na y entropía en cada línea y en el ciclo: 1) Suponiendo isoterma la
de tiempo por la varilla. 2) Determinar las variaciones de entropía de transformación (1 ® 2). 2) Suponiendo adiabática la transformación
los dos focos térmicos (a 500 K y 300 K), de la barra metálica y del uni- (1 ® 2).