Page 212 - Quimica - Undécima Edición

182 CAPÍTULO 5 Gases

mostraron que, a una presión constante, el volumen de una muestra de gas se expande
cuando se calienta y se contrae al enfriarse (fi gura 5.8). Las relaciones cuantitativas im-
Tubo
capilar plicadas en estos cambios de temperatura y volumen del gas resultan ser notablemente
congruentes. Por ejemplo, observamos un fenómeno interesante cuando estudiamos la
relación entre temperatura y volumen a varias presiones. A cualquier presión dada,
Mercurio
la gráfi ca de volumen en relación con la temperatura es una línea recta. Al extender la
Gas recta al volumen cero, encontramos que la intersección en el eje de temperatura tiene un
valor de 2273.158C. A cualquier otra presión obtenemos una recta diferente para la grá-
fi ca de volumen y temperatura, pero alcanzamos la misma intersección de 2273.158C
Temperatura Temperatura para la temperatura correspondiente al volumen cero (fi gura 5.9). (En la práctica, podemos
baja alta
medir el volumen de un gas sólo en un intervalo limitado de temperatura, ya que todos
los gases se condensan a bajas temperaturas para formar líquidos.)
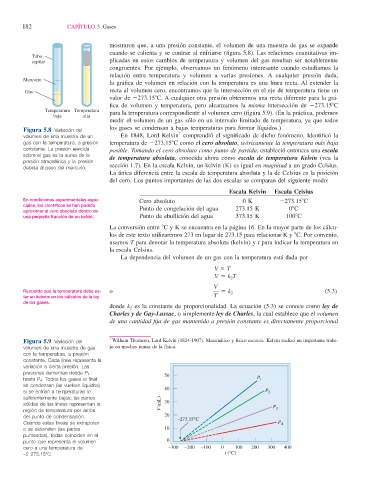
Figura 5.8 Variación del 7
volumen de una muestra de un En 1848, Lord Kelvin comprendió el signifi cado de dicho fenómeno. Identifi có la
gas con la temperatura, a presión temperatura de 2273.158C como el cero absoluto , teóricamente la temperatura más baja
constante. La presión ejercida posible. Tomando el cero absoluto como punto de partida, estableció entonces una escala
sobre el gas es la suma de la de temperatura absoluta , conocida ahora como escala de temperatura Kelvin (vea la
presión atmosférica y la presión
debida al peso del mercurio. sección 1.7). En la escala Kelvin, un kelvin (K) es igual en magnitud a un grado Celsius.
La única diferencia entre la escala de temperatura absoluta y la de Celsius es la posición
del cero. Los puntos importantes de las dos escalas se comparan del siguiente modo:
Escala Kelvin Escala Celsius
En condiciones experimentales espe- Cero absoluto 0 K 2273.158C
ciales, los científi cos se han podido
aproximar al cero absoluto dentro de Punto de congelación del agua 273.15 K 08C
una pequeña fracción de un kelvin. Punto de ebullición del agua 373.15 K 1008C
La conversión entre 8C y K se encuentra en la página 16. En la mayor parte de los cálcu-
los de este texto utilizaremos 273 en lugar de 273.15 para relacionar K y 8C. Por convenio,
usamos T para denotar la temperatura absoluta (kelvin) y t para indicar la temperatura en
la escala Celsius.
La dependencia del volumen de un gas con la temperatura está dada por

V ~ T
V 5 k 2 T
V
Recuerde que la temperatura debe es- o 5 k 2 (5.3)
tar en kelvins en los cálculos de la ley T
de los gases.
donde k 2 es la constante de proporcionalidad. La ecuación (5.3) se conoce como ley de
Charles y de Gay-Lussac , o simplemente ley de Charles , la cual establece que el volumen
de una cantidad fi ja de gas mantenido a presión constante es directamente proporcional

7
Figura 5.9 Variación del William Thomson, Lord Kelvin (1824-1907). Matemático y físico escocés. Kelvin realizó un importante traba-
volumen de una muestra de gas jo en muchas ramas de la física.
con la temperatura, a presión
constante. Cada línea representa la
variación a cierta presión. Las
presiones aumentan desde P 1
50
hasta P 4 . Todos los gases al fi nal P 1
se condensan (se vuelven líquidos) 40
si se enfrían a temperaturas lo P 2
sufi cientemente bajas; las partes
sólidas de las líneas representan la V (mL) 30 P
región de temperatura por arriba 3
del punto de condensación. 20
–273.15°C
Cuando estas líneas se extrapolan P 4
o se extienden (las partes 10
punteadas), todas coinciden en el
punto que representa el volumen 0
cero a una temperatura de –300 –200 –100 0 100 200 300 400
–2 273.158C. t (°C)