Page 652 - Física Tippens: Conceptos y Aplicaciones, Séptima Edición Revisada

32.6 Circuitos en serie de ca 633

Observe a partir del diagrama de fase que un valor de VL que sea mayor que Vc resulta en
un ángulo de fase positivo. En otras palabras, si el circuito es inductivo, el voltaje se adelanta
a la corriente. En un circuito capacitivo, Xc > Xv y resultará un ángulo de fase negativo, lo
que indica que el voltaje está atrasado respecto a la corriente. En cualquier caso, la magnitud
del ángulo de fase puede determinarse a partir de

V, - Vr
tan O = —------ - (32.28)
Vr
Una forma más útil de la ecuación (32.27) se obtiene recordando que

= iR V, = iXL Vc = iXc

Después de realizar las sustituciones queda como

V = ¿VR2 + (XL - Xcf (32.29)
La cantidad multiplicada por la corriente en la ecuación (32.29) es una medida de la oposi­
ción combinada que ofrece el circuito a la corriente alterna. Se denomina la impedancia y se
expresa por medio del símbolo Z.

Z = VR2 {XL - Xc)2 (32.30)
+
Cuanto mayor es la impedancia en un circuito, menor es la corriente producida por el voltaje.
Puesto que R , X y Xc se miden en ohms, la impedancia también se expresa en ohms.
Por consiguiente, la corriente efectiva i en un circuito de ca se obtiene por medio de
V
i = - (32.31)

donde V = voltaje aplicado
Z = impedancia de circuito
Conviene recordar que Z depende de la frecuencia de la corriente alterna, así como de la
resistencia, la inductancia y la capacitancia.
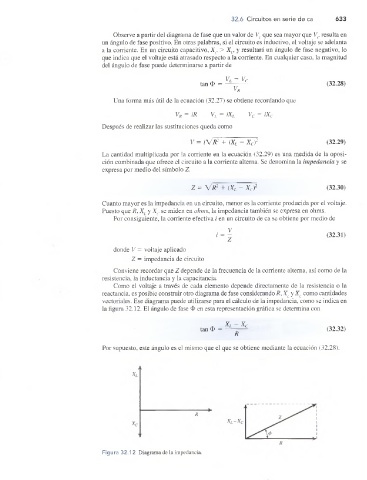
Como el voltaje a través de cada elemento depende directamente de la resistencia o la
reactancia, es posible construir otro diagrama de fase considerando R, XL y Xc como cantidades
vectoriales. Ese diagrama puede utilizarse para el cálculo de la impedancia, como se indica en
la figura 32.12. El ángulo de fase O en esta representación gráfica se determina con

tan <í> = Xl ~ Xc (32.32)
R
Por supuesto, este ángulo es el mismo que el que se obtiene mediante la ecuación (32.28).

Figura 32.1 2 Diagrama de la impedancia.