Page 472 - Fisica General Burbano
P. 472
486 EL CAMPO MAGNÉTICO
Considerada la anterior representación, se llama FLUJO DE INDUCCIÓN MAGNÉTICA a través de una
superficie al número de líneas de campo que atraviesan a ésta.
En la Fig. XXI-33 el número de líneas de campo que atraviesan a la superficie dA es el mismo
que el que atraviesa a dA¢(proyección de dA sobre la superficie normal al campo); como B es el
número de líneas de fuerza que atraviesan a la unidad de superficie normal al campo, a dA le
atravesarán:
d f =BdA¢ (11)
pero como: dA¢=dA cos j, nos queda para valor del flujo a través de dA:
z
Fig. XXI-33. dA¢es la proyección d f = Bd A cos j =B ? dA Û f = B ? dA
de dA sobre el plano normal al vec- A
tor inducción magnética.
2
Haciendo B =1T =1 N/A · m, A =1 m y cos j =1, obtenemos para la unidad de flujo en
el SI: 1 WEBER (Wb) =1N · m/A
Podemos definir la inducción magnética como el flujo por unidad de área normal al campo
(fórmula 11), o DENSIDAD SUPERFICIAL DE FLUJO. Con tal criterio, se le llama también a la unidad del
SI de inducción magnética Wb/m .
2
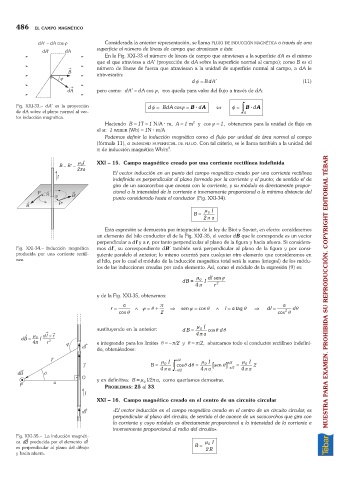
XXI 15. Campo magnético creado por una corriente rectilínea indefinida
El vector inducción en un punto del campo magnético creado por una corriente rectilínea
indefinida es perpendicular al plano formado por la corriente y el punto; de sentido el de
giro de un sacacorchos que avanza con la corriente, y su módulo es directamente propor-
cional a la intensidad de la corriente e inversamente proporcional a la mínima distancia del
punto considerado hasta el conductor (Fig. XXI-34).
m I
B = 0
2 p a
Esta expresión se demuestra por integración de la ley de Biot y Savart, en efecto: consideremos
un elemento del hilo conductor dl de la Fig. XXI-35, el vector dB que le corresponde es un vector
perpendicular a dl y a r, por tanto perpendicular al plano de la figura y hacia afuera. Si considera-
Fig. XXI-34. Inducción magnética mos dl¢, su correspondiente dB¢también será perpendicular al plano de la figura y por consi-
producida por una corriente rectilí- guiente paralelo al anterior; lo mismo ocurrirá para cualquier otro elemento que consideremos en
nea. el hilo, por lo cual el módulo de la inducción magnética total será la suma (integral) de los módu-
los de las inducciones creadas por cada elemento. Así, como el módulo de la expresión (9) es:
m 0 dl sen j
dB = I
4 p r 2
y de la Fig. XXI-35, obtenemos: MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
a p a
r = Ù j = q + Þ se n j = cos q Ù l a=tag q Þ dl = 2 dq
cos q 2 cos q
sustituyendo en la anterior: dB = m 0 I cos q d q
4 p a
e integrando para los límites q =p/2 y q =p/2, abarcamos todo el conductor rectilíneo indefini-
do, obteniéndose:
I
m az p 2 / m I p 2/ m I
d
B = 0 cos qq = 0 sen q = 0 2
4 p -p 2 / 4 p a -p 2/ 4 p a
y en definitiva: B =m I/2pa, como queríamos demostrar.
0
PROBLEMAS:25 al 33.
XXI 16. Campo magnético creado en el centro de un circuito circular
«El vector inducción en el campo magnético creado en el centro de un circuito circular, es
perpendicular al plano del circuito, de sentido el de avance de un sacacorchos que gira con
la corriente y cuyo módulo es directamente proporcional a la intensidad de la corriente e
inversamente proporcional al radio del circuito».
Fig. XXI-35. La inducción magnéti-
®
ca dB producida por el elemento dl ® m 0 I
es perpendicular al plano del dibujo B = 2 R
y hacia afuera.