Page 442 - Fisica General Burbano

CORRIENTES NO ESTACIONARIAS. CORRIENTE DE DESPLAZAMIENTO 455

qt()
Vt() = = RI t()
C
siendo q (t) e I (t), la carga del condensador y la intensidad de corriente en dicho instante; el con-
densador «pierde carga» a razón de:
dq
It() =-
dt
q dq dq dt
que sustituida en la anterior nos queda: =- R Þ = -
C dt q RC
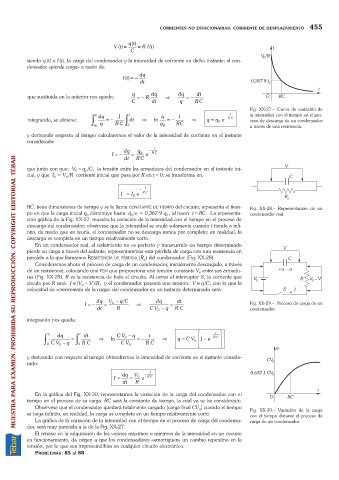
q z
la intensidad con el tiempo en el pro-
q dq R Cz t q t - t Fig. XX-27.– Curva de variación de
1
integrando, se obtiene: =- dt Þ ln = - Þ q = q e RC ceso de descarga de un condensador
0
q 0 0 q 0 RC a través de una resistencia.
y derivando respecto al tiempo calcularemos el valor de la intensidad de corriente en el instante
considerado:
dq q - t
I =- = 0 e RC
dt RC
MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
que junto con que: V =q /C, la tensión entre las armaduras del condensador en el instante ini-
0
0
cial, y que I = V /R corriente inicial que pasa por R en t =0; se transforma en:
0
0
t
- RC
I = I e
0
RC, tiene dimensiones de tiempo y se le llama CONSTANTE DE TIEMPO del circuito; representa el tiem- Fig. XX-28.– Representación de un
po en que la carga inicial q disminuye hasta q /e = 0,367 9 q , al hacer t =RC. La representa- condensador real.
0
0
0
ción gráfica de la Fig. XX-27, muestra la variación de la intensidad con el tiempo en el proceso de
descarga del condensador; obsérvese que la intensidad se anula solamente cuando t tiende a infi-
nito, de modo que en teoría, el condensador no se descarga nunca por completo; en realidad, la
descarga es completa en un tiempo relativamente corto.
En un condensador real, el aislamiento no es perfecto y transcurrido un tiempo determinado
pierde su carga a través del aislante; representaremos esta pérdida de carga con una resistencia en
paralelo a la que llamamos RESISTENCIA DE PÉRDIDA (R ) del condensador (Fig. XX-28).
p
Consideremos ahora el proceso de carga de un condensador, inicialmente descargado, a través
de un resistencia, colocando una FEM que proporciona una tensión constante V entre sus armadu-
0
ras (Fig. XX-29). R es la resistencia de todo el circuito. Al cerrar el interruptor S, la corriente que
circula por R será: I =(V – V)/R, y el condensador poseerá una tensión: V =q/C, con lo que la
0
velocidad de «crecimiento de la carga» del condensador en un instante determinado será:
q C
dq V - / dq dt
I =- = 0 Þ = Fig. XX-29.– Proceso de carga de un
dt R CV - q RC condensador.
0
integrando nos queda:
t
q dq t dt CV 0 -q t é - RC ù
1
ò CV 0 -q = 0 R Þ ln C V 0 = - R C Þ q =C V 0 ê - e ú
ò C
ê
ú
0
ë
û
y derivando con respecto al tiempo obtendremos la intensidad de corriente en el instante conside-
rado:
t
dq V - RC
I = = 0 e
dt R
En la gráfica del Fig. XX-30, representamos la variación de la carga del condensador con el
tiempo en el proceso de su carga. RC será la constante de tiempo, la cual ya se ha considerado.
Obsérvese que el condensador quedará totalmente cargado (carga final CV ) cuando el tiempo Fig. XX-30.– Variación de la carga
0
se haga infinito, en realidad, la carga es completa en un tiempo relativamente corto. con el tiempo durante el proceso de
La gráfica de la variación de la intensidad con el tiempo en el proceso de carga del condensa- carga de un condensador.
dor, será muy parecida a la de la Fig. XX-27.
El retraso en la adquisición de los valores máximos o mínimos de la intensidad en un circuito
en funcionamiento, da origen a que los condensadores «amortigüen» un cambio repentino en la
tensión, por lo que son imprescindibles en cualquier circuito electrónico.
PROBLEMAS:85 al 88.