Page 11 - Fisica General Burbano

18 FÍSICA. MAGNITUDES FÍSICAS. SISTEMAS DE UNIDADES. ERRORES EN LAS MEDIDAS

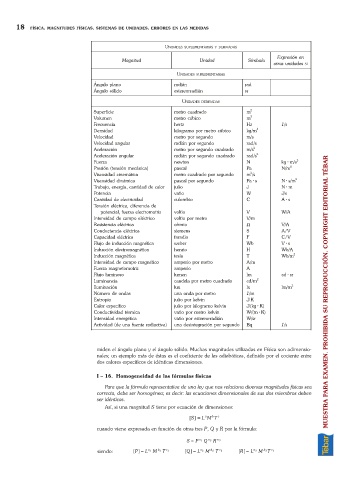
UNIDADES SUPLEMENTARIAS Y DERIVADAS
Expresión en
Magnitud Unidad Símbolo
otras unidades SI
UNIDADES SUPLEMENTARIAS
Ángulo plano radián rad
Ángulo sólido estereorradián sr

UNIDADES DERIVADAS
Superficie metro cuadrado m 2
Volumen metro cúbico m 3
Frecuencia hertz Hz 1/s
Densidad kilogramo por metro cúbico kg/m 3
Velocidad metro por segundo m/s
Velocidad angular radián por segundo rad/s
Aceleración metro por segundo cuadrado m/s 2
Aceleración angular radián por segundo cuadrado rad/s 2
Fuerza newton N kg · m/s 2
Presión (tensión mecánica) pascal Pa N/m 2
2
Viscosidad cinemática metro cuadrado por segundo m /s
Viscosidad dinámica pascal por segundo Pa · s N · s/m 2
Trabajo, energía, cantidad de calor julio J N · m
Potencia vatio W J/s
Cantidad de electricidad culombio C A · s
Tensión eléctrica, diferencia de
potencial, fuerza electromotriz voltio V W/A
Intensidad de campo eléctrico voltio por metro V/m
Resistencia eléctrica ohmio W V/A
Conductancia eléctrica siemens S A / V
Capacidad eléctrica faradio F C / V
Flujo de inducción magnética weber Wb V · s
Inducción electromagnética henrio H Wb/A
Inducción magnética tesla T Wb/m 2
Intensidad de campo magnético amperio por metro A/m
Fuerza magnetomotriz amperio A
Flujo luminoso lumen lm cd · sr
Luminancia candela por metro cuadrado cd/m 2
Iluminación lux lx lm/m 2
Número de ondas una onda por metro 1/m MUESTRA PARA EXAMEN. PROHIBIDA SU REPRODUCCIÓN. COPYRIGHT EDITORIAL TÉBAR
Entropía julio por kelvin J/ K
Calor específico julio por kilogramo kelvin J/(kg · K)
Conductividad térmica vatio por metro kelvin W/(m · K)
Intensidad energética vatio por estereorradián W/sr
Actividad (de una fuente radiactiva) una desintegración por segundo Bq 1/s

miden el ángulo plano y el ángulo sólido. Muchas magnitudes utilizadas en Física son adimensio-
nales; un ejemplo más de éstas es el coeficiente de las adiabáticas, definido por el cociente entre
dos calores específicos de idénticas dimensiones.

I – 16. Homogeneidad de las fórmulas físicas
Para que la fórmula representativa de una ley que nos relaciona diversas magnitudes físicas sea
correcta, debe ser homogénea; es decir: las ecuaciones dimensionales de sus dos miembros deben
ser idénticas.
Así, si una magnitud S tiene por ecuación de dimensiones:

a
b
[S] =L M T c
cuando viene expresada en función de otras tres P, Q y R por la fórmula:
S = P x 1 Q x 2 R x 3
siendo: []P = L M b 1 T c 1 [ ]Q = L a 2 M b 2 T c 2 [ ]R = L a 3 M b 3 T c 3
a 1