Page 166 - Libro Hipertextos Fisica 1

Rotación de sólidos

EJEMPLOS

1. Una barra homogénea de 2 m de largo y peso l
100 N está sujeta por uno de sus extremos a una 2 2 ? mg ? sen 37° 1 l ? T ? sen 53° 1 0 5 0
pared vertical por medio de una cuerda. El otro 2 m
extremo está sujeto al piso por medio de un 2 2 ?100 N ? sen 37° 1 2 m ? T ? sen 53° 5 0
pivote. Determinar: T 5 37,7 N
La tensión que soporta la cuerda y la fuerza ejer- Como F 5 T tenemos que F 5 37,7 N.
cida por el pivote O sobre la barra. x x
Por tanto, la tensión que ejerce la cuerda es 37,7 N
y la fuerza ejercida por el pivote corresponde al
vector (37,7; 100) con sus componentes medidas
en N, cuya norma es 107 N y forma con el piso un
ángulo de 69°.
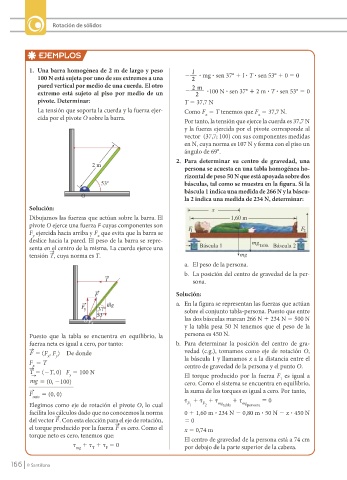
2. Para determinar su centro de gravedad, una
P
persona se acuesta en una tabla homogénea ho-
rizontal de peso 50 N que está apoyada sobre dos
ž básculas, tal como se muestra en la figura. Si la
báscula 1 indica una medida de 266 N y la báscu-
2
la 2 indica una medida de 234 N, determinar:
Solución: x
Dibujamos las fuerzas que actúan sobre la barra. El 1,60 m
pivote O ejerce una fuerza F cuyas componentes son F F
F ejercida hacia arriba y F que evita que la barra se 1 2
x
y
deslice hacia la pared. El peso de la barra se repre- mg
senta en el centro de la misma. La cuerda ejerce una Báscula 1 Tabla Báscula 2
tensión T, cuya norma es T. mg
a. El peso de la persona.
b. La posición del centro de gravedad de la per-
sona.

Solución:
a. En la figura se representan las fuerzas que actúan
sobre el conjunto tabla-persona. Puesto que entre
las dos básculas marcan 266 N 1 234 N 5 500 N
y la tabla pesa 50 N tenemos que el peso de la
Puesto que la tabla se encuentra en equilibrio, la persona es 450 N.
fuerza neta es igual a cero, por tanto: b. Para determinar la posición del centro de gra-
F 5 (F , F ) De donde vedad (c.g.), tomamos como eje de rotación O,
x y la báscula 1 y llamamos x a la distancia entre el
F 5 T centro de gravedad de la persona y el punto O.
x
T 5 (2T, 0) F 5 100 N
y El torque producido por la fuerza F es igual a
1
mg 5 (0, 2100) cero. Como el sistema se encuentra en equilibrio,
F neta 5 (0, 0) la suma de los torques es igual a cero. Por tanto,
F
F
Elegimos como eje de rotación el pivote O, lo cual t 1 t 1 t mg tabla 1 τ mg persona 5 0
2
1
facilita los cálculos dado que no conocemos la norma 0 1 1,60 m ? 234 N 2 0,80 m ? 50 N 2 x ? 450 N
del vector F. Con esta elección para el eje de rotación, 5 0
el torque producido por la fuerza F es cero. Como el x 5 0,74 m
torque neto es cero, tenemos que: El centro de gravedad de la persona está a 74 cm
t 1 t 1 t 5 0
mg T F por debajo de la parte superior de la cabeza.

166 © Santillana

FI10-U5(136-167).indd 166 4/10/10 14:05